Question Number 29167 by abdo imad last updated on 04/Feb/18
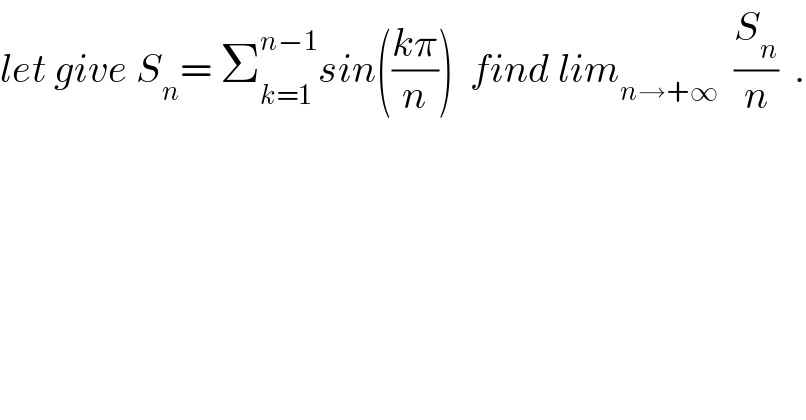
$${let}\:{give}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}−\mathrm{1}} {sin}\left(\frac{{k}\pi}{{n}}\right)\:\:{find}\:{lim}_{{n}\rightarrow+\infty} \:\:\frac{{S}_{{n}} }{{n}}\:\:. \\ $$
Commented by abdo imad last updated on 08/Feb/18

$${S}_{{n}} ={Im}\left(\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{e}^{{i}\frac{{k}\pi}{{n}}} \right)\:\:\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\:{e}^{{i}\frac{{k}\pi}{{n}}} \:=\:\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:\left({e}^{{i}\frac{\pi}{{n}}} \right)^{{k}} =\frac{\mathrm{1}−\:{e}^{{i}\pi} }{\mathrm{1}−\:{e}^{{i}\frac{\pi}{{n}}} }=\frac{\mathrm{2}}{\mathrm{1}−{cos}\left(\frac{\pi}{{n}}\right)−{isin}\left(\frac{\pi}{{n}}\right)} \\ $$$$=\:\:\:\:\frac{\mathrm{2}}{\mathrm{2}{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{2}{n}}\right)\:−\mathrm{2}{isin}\left(\frac{\pi}{\mathrm{2}{n}}\right){cos}\left(\frac{\pi}{\mathrm{2}{n}}\right)} \\ $$$$=\:\:\:\frac{\mathrm{1}}{−{isin}\left(\frac{\pi}{\mathrm{2}{n}}\right)\left({e}^{{i}\frac{\pi}{\mathrm{2}{n}}} \right)}=\frac{{i}\:{e}^{−{i}\frac{\pi}{\mathrm{2}{n}}} }{{sin}\left(\frac{\pi}{\mathrm{2}{n}}\right)}={i}\frac{{cos}\left(\frac{\pi}{\mathrm{2}{n}}\right)\:−{isin}\left(\frac{\pi}{\mathrm{2}{n}}\right)}{{sin}\left(\frac{\pi}{\mathrm{2}{n}}\right)}\:\Rightarrow \\ $$$${S}_{{n}} =\:\frac{\mathrm{1}}{{tan}\left(\frac{\pi}{\mathrm{2}{n}}\right)}\:\:{we}\:{have}\:\:\frac{{S}_{{n}} }{{n}}=\:\frac{\mathrm{1}}{{ntan}\left(\frac{\pi}{\mathrm{2}{n}}\right)} \\ $$$${but}\:{tan}\left(\frac{\pi}{\mathrm{2}{n}}\right)\sim\:\frac{\pi}{\mathrm{2}{n}}\:\left({n}\rightarrow+\infty\right)\:{and}\:{n}\:{tan}\left(\frac{\pi}{\mathrm{2}{n}}\right)\sim\:\frac{\pi}{\mathrm{2}}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:\:\frac{{S}_{{n}} }{{n}}\:=\:\frac{\mathrm{2}}{\pi}\:\:. \\ $$
