Question Number 27189 by abdo imad last updated on 02/Jan/18
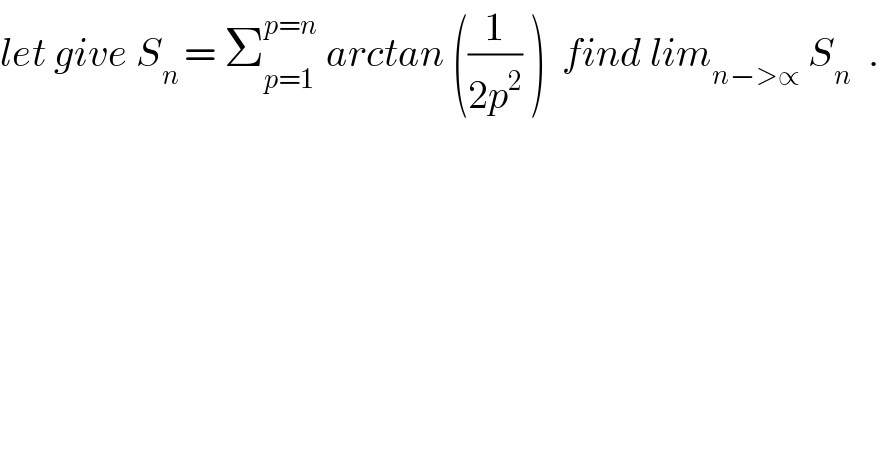
$${let}\:{give}\:{S}_{{n}\:} =\:\sum_{{p}=\mathrm{1}} ^{{p}={n}} \:{arctan}\:\left(\frac{\mathrm{1}}{\mathrm{2}{p}^{\mathrm{2}} }\:\right)\:\:{find}\:{lim}_{{n}−>\propto} \:{S}_{{n}} \:\:. \\ $$
Answered by prakash jain last updated on 03/Jan/18
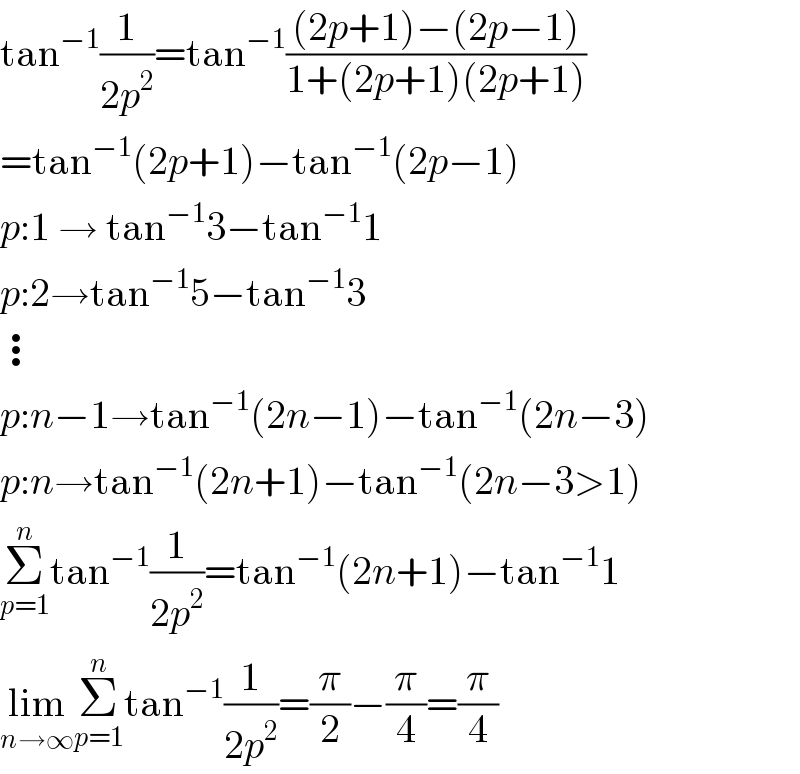
$$\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{p}^{\mathrm{2}} }=\mathrm{tan}^{−\mathrm{1}} \frac{\left(\mathrm{2}{p}+\mathrm{1}\right)−\left(\mathrm{2}{p}−\mathrm{1}\right)}{\mathrm{1}+\left(\mathrm{2}{p}+\mathrm{1}\right)\left(\mathrm{2}{p}+\mathrm{1}\right)} \\ $$$$=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{p}+\mathrm{1}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{p}−\mathrm{1}\right) \\ $$$${p}:\mathrm{1}\:\rightarrow\:\mathrm{tan}^{−\mathrm{1}} \mathrm{3}−\mathrm{tan}^{−\mathrm{1}} \mathrm{1} \\ $$$${p}:\mathrm{2}\rightarrow\mathrm{tan}^{−\mathrm{1}} \mathrm{5}−\mathrm{tan}^{−\mathrm{1}} \mathrm{3} \\ $$$$\vdots \\ $$$${p}:{n}−\mathrm{1}\rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{n}−\mathrm{1}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{n}−\mathrm{3}\right) \\ $$$${p}:{n}\rightarrow\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{n}−\mathrm{3}>\mathrm{1}\right) \\ $$$$\underset{{p}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{p}^{\mathrm{2}} }=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{2}{n}+\mathrm{1}\right)−\mathrm{tan}^{−\mathrm{1}} \mathrm{1} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{p}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}{p}^{\mathrm{2}} }=\frac{\pi}{\mathrm{2}}−\frac{\pi}{\mathrm{4}}=\frac{\pi}{\mathrm{4}} \\ $$
