Menu Close

let-give-S-x-n-1-x-n-n-and-W-x-n-1-1-n-x-n-n-2-calculate-S-x-W-x-in-that-we-know-x-lt-1-

Tinku Tara 0 Comments
Pin




Question Number 27098 by abdo imad last updated on 02/Jan/18
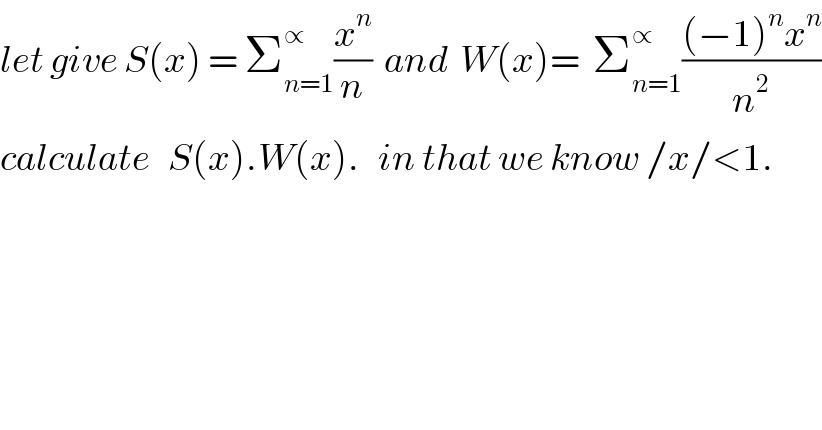
let give S(x) = Σ_(n=1) ^∝ (x^n /n) and W(x)= Σ_(n=1) ^∝ (((−1)^n x^n )/n^2 ) calculate S(x).W(x). in that we know /x/<1.
$${let}\:{give}\:{S}\left({x}\right)\:=\:\sum_{{n}=\mathrm{1}} ^{\propto} \frac{{x}^{{n}} }{{n}}\:\:{and}\:\:{W}\left({x}\right)=\:\:\sum_{{n}=\mathrm{1}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} }{{n}^{\mathrm{2}} } \\ $$$${calculate}\:\:\:{S}\left({x}\right).{W}\left({x}\right).\:\:\:{in}\:{that}\:{we}\:{know}\:/{x}/<\mathrm{1}. \\ $$
Commented by prakash jain last updated on 02/Jan/18
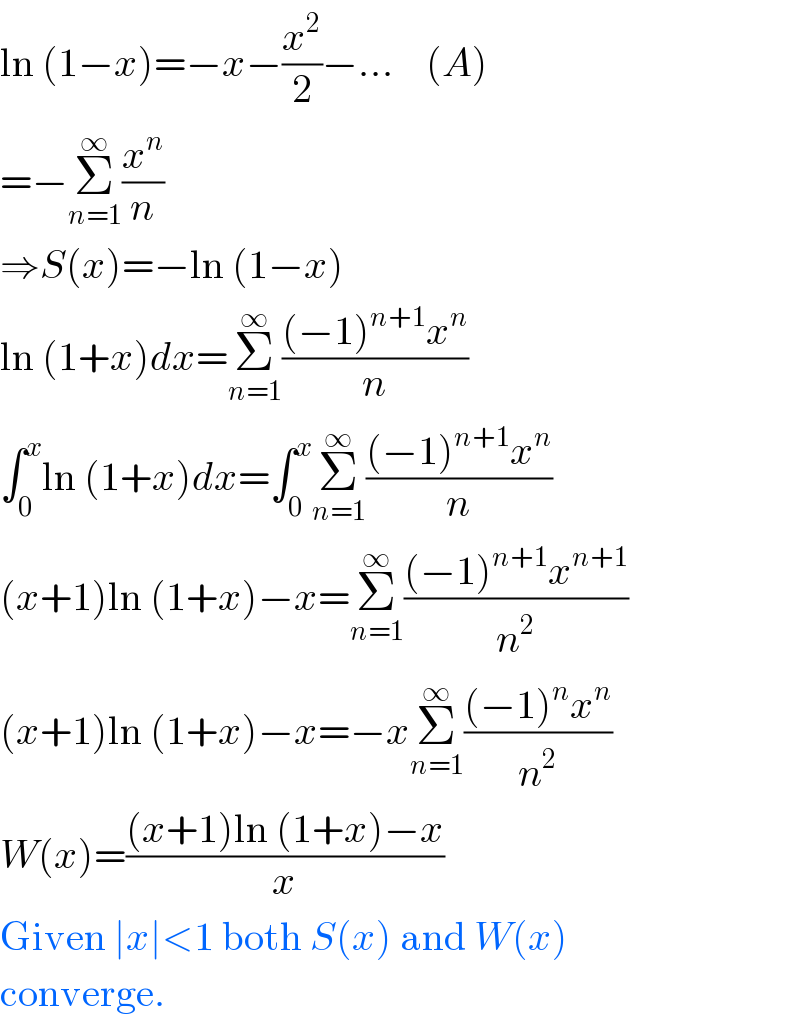
ln (1−x)=−x−(x^2 /2)−... (A) =−Σ_(n=1) ^∞ (x^n /n) ⇒S(x)=−ln (1−x) ln (1+x)dx=Σ_(n=1) ^∞ (((−1)^(n+1) x^n )/n) ∫_0 ^x ln (1+x)dx=∫_0 ^x Σ_(n=1) ^∞ (((−1)^(n+1) x^n )/n) (x+1)ln (1+x)−x=Σ_(n=1) ^∞ (((−1)^(n+1) x^(n+1) )/n^2 ) (x+1)ln (1+x)−x=−xΣ_(n=1) ^∞ (((−1)^n x^n )/n^2 ) W(x)=(((x+1)ln (1+x)−x)/x) Given ∣x∣<1 both S(x) and W(x) converge.
$$\mathrm{ln}\:\left(\mathrm{1}−{x}\right)=−{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}−…\:\:\:\:\left({A}\right) \\ $$$$=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}} \\ $$$$\Rightarrow{S}\left({x}\right)=−\mathrm{ln}\:\left(\mathrm{1}−{x}\right) \\ $$$$\mathrm{ln}\:\left(\mathrm{1}+{x}\right){dx}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{{n}} }{{n}}\: \\ $$$$\int_{\mathrm{0}} ^{{x}} \mathrm{ln}\:\left(\mathrm{1}+{x}\right){dx}=\int_{\mathrm{0}} ^{{x}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{{n}} }{{n}}\: \\ $$$$\left({x}+\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{1}+{x}\right)−{x}=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} {x}^{{n}+\mathrm{1}} }{{n}^{\mathrm{2}} } \\ $$$$\left({x}+\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{1}+{x}\right)−{x}=−{x}\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} {x}^{{n}} }{{n}^{\mathrm{2}} } \\ $$$${W}\left({x}\right)=\frac{\left({x}+\mathrm{1}\right)\mathrm{ln}\:\left(\mathrm{1}+{x}\right)−{x}}{{x}} \\ $$$$\mathrm{Given}\:\mid{x}\mid<\mathrm{1}\:\mathrm{both}\:{S}\left({x}\right)\:\mathrm{and}\:{W}\left({x}\right) \\ $$$$\mathrm{converge}. \\ $$
Commented by abdo imad last updated on 04/Jan/18
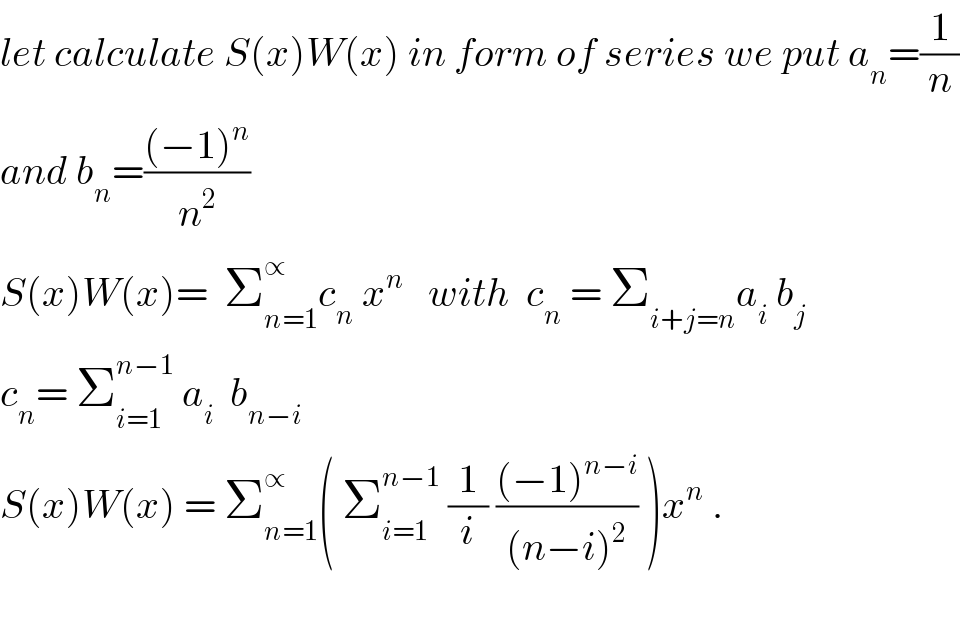
let calculate S(x)W(x) in form of series we put a_n =(1/n) and b_n =(((−1)^n )/n^2 ) S(x)W(x)= Σ_(n=1) ^∝ c_n x^n with c_n = Σ_(i+j=n) a_i b_j c_n = Σ_(i=1) ^(n−1) a_i b_(n−i) S(x)W(x) = Σ_(n=1) ^∝ ( Σ_(i=1) ^(n−1) (1/i) (((−1)^(n−i) )/((n−i)^2 )) )x^n .
$${let}\:{calculate}\:{S}\left({x}\right){W}\left({x}\right)\:{in}\:{form}\:{of}\:{series}\:{we}\:{put}\:{a}_{{n}} =\frac{\mathrm{1}}{{n}} \\ $$$${and}\:{b}_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}^{\mathrm{2}} } \\ $$$${S}\left({x}\right){W}\left({x}\right)=\:\:\sum_{{n}=\mathrm{1}} ^{\propto} {c}_{{n}} \:{x}^{{n}} \:\:\:{with}\:\:{c}_{{n}} \:=\:\sum_{{i}+{j}={n}} {a}_{{i}} \:{b}_{{j}} \\ $$$${c}_{{n}} =\:\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} \:{a}_{{i}} \:\:{b}_{{n}−{i}} \\ $$$${S}\left({x}\right){W}\left({x}\right)\:=\:\sum_{{n}=\mathrm{1}} ^{\propto} \left(\:\sum_{{i}=\mathrm{1}} ^{{n}−\mathrm{1}} \:\frac{\mathrm{1}}{{i}}\:\frac{\left(−\mathrm{1}\right)^{{n}−{i}} }{\left({n}−{i}\right)^{\mathrm{2}} }\:\right){x}^{{n}} \:. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *