Menu Close

let-give-the-sequence-V-n-k-1-k-n-1-k-2-n-2-1-n-find-the-value-of-lim-n-gt-V-n-

Tinku Tara 0 Comments
Pin




Question Number 27664 by abdo imad last updated on 12/Jan/18
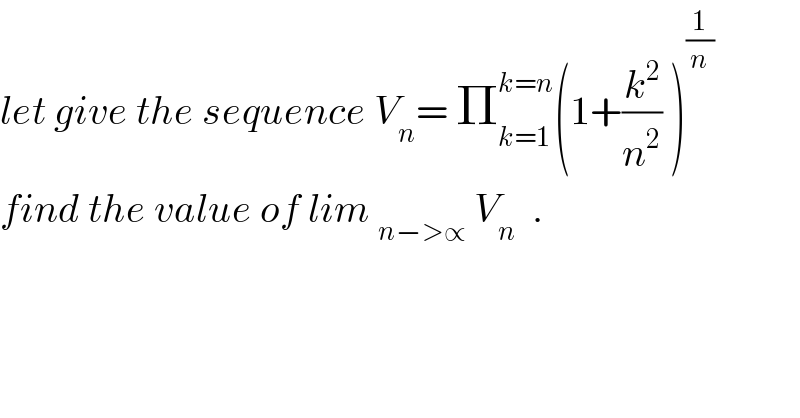
let give the sequence V_n = Π_(k=1) ^(k=n) (1+(k^2 /n^2 ) )^(1/n) find the value of lim _(n−>∝) V_n .
$${let}\:{give}\:{the}\:{sequence}\:{V}_{{n}} =\:\prod_{{k}=\mathrm{1}} ^{{k}={n}} \left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\:\right)^{\frac{\mathrm{1}}{{n}}} \\ $$$${find}\:{the}\:{value}\:{of}\:{lim}\:_{{n}−>\propto} \:{V}_{{n}} \:\:. \\ $$
Commented by abdo imad last updated on 14/Jan/18
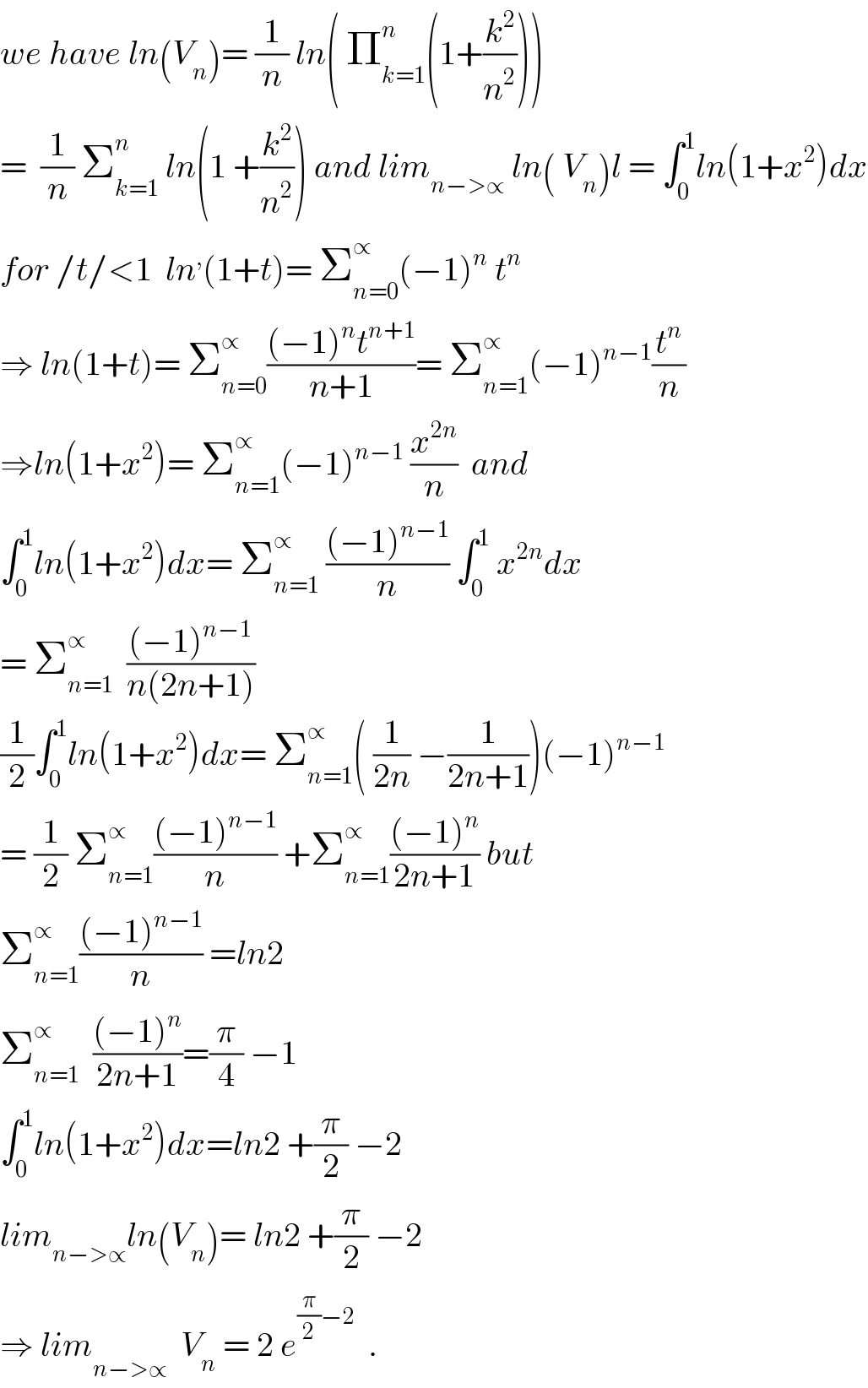
we have ln(V_n )= (1/n) ln( Π_(k=1) ^n (1+(k^2 /n^2 ))) = (1/n) Σ_(k=1) ^(n ) ln(1 +(k^2 /n^2 )) and lim_(n−>∝) ln( V_n )l = ∫_0 ^1 ln(1+x^2 )dx for /t/<1 ln^, (1+t)= Σ_(n=0) ^∝ (−1)^n t^n ⇒ ln(1+t)= Σ_(n=0) ^∝ (((−1)^n t^(n+1) )/(n+1))= Σ_(n=1) ^∝ (−1)^(n−1) (t^n /n) ⇒ln(1+x^2 )= Σ_(n=1) ^∝ (−1)^(n−1) (x^(2n) /n) and ∫_0 ^1 ln(1+x^2 )dx= Σ_(n=1) ^∝ (((−1)^(n−1) )/n) ∫_0 ^1 x^(2n) dx = Σ_(n=1) ^∝ (((−1)^(n−1) )/(n(2n+1))) (1/2)∫_0 ^1 ln(1+x^2 )dx= Σ_(n=1) ^∝ ( (1/(2n)) −(1/(2n+1)))(−1)^(n−1) = (1/2) Σ_(n=1) ^∝ (((−1)^(n−1) )/n) +Σ_(n=1) ^∝ (((−1)^n )/(2n+1)) but Σ_(n=1) ^∝ (((−1)^(n−1) )/n) =ln2 Σ_(n=1) ^∝ (((−1)^n )/(2n+1))=(π/4) −1 ∫_0 ^1 ln(1+x^2 )dx=ln2 +(π/2) −2 lim_(n−>∝) ln(V_n )= ln2 +(π/2) −2 ⇒ lim_(n−>∝^ ) V_n = 2 e^((π/2)−2) .
$${we}\:{have}\:{ln}\left({V}_{{n}} \right)=\:\frac{\mathrm{1}}{{n}}\:{ln}\left(\:\prod_{{k}=\mathrm{1}} ^{{n}} \left(\mathrm{1}+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\right) \\ $$$$=\:\:\frac{\mathrm{1}}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}\:} \:{ln}\left(\mathrm{1}\:+\frac{{k}^{\mathrm{2}} }{{n}^{\mathrm{2}} }\right)\:{and}\:{lim}_{{n}−>\propto} \:{ln}\left(\:{V}_{{n}} \right){l}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx} \\ $$$${for}\:/{t}/<\mathrm{1}\:\:{ln}^{,} \left(\mathrm{1}+{t}\right)=\:\sum_{{n}=\mathrm{0}} ^{\propto} \left(−\mathrm{1}\right)^{{n}} \:{t}^{{n}} \\ $$$$\Rightarrow\:{ln}\left(\mathrm{1}+{t}\right)=\:\sum_{{n}=\mathrm{0}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}} {t}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}=\:\sum_{{n}=\mathrm{1}} ^{\propto} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \frac{{t}^{{n}} }{{n}} \\ $$$$\Rightarrow{ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)=\:\sum_{{n}=\mathrm{1}} ^{\propto} \left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \:\frac{{x}^{\mathrm{2}{n}} }{{n}}\:\:{and} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}=\:\sum_{{n}=\mathrm{1}} ^{\propto} \:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\mathrm{2}{n}} {dx} \\ $$$$=\:\sum_{{n}=\mathrm{1}} ^{\propto} \:\:\frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}\left(\mathrm{2}{n}+\mathrm{1}\right)} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}=\:\sum_{{n}=\mathrm{1}} ^{\propto} \left(\:\frac{\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:\sum_{{n}=\mathrm{1}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:+\sum_{{n}=\mathrm{1}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}\:{but} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\propto} \frac{\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{{n}}\:={ln}\mathrm{2} \\ $$$$\sum_{{n}=\mathrm{1}} ^{\propto} \:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}{n}+\mathrm{1}}=\frac{\pi}{\mathrm{4}}\:−\mathrm{1} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {ln}\left(\mathrm{1}+{x}^{\mathrm{2}} \right){dx}={ln}\mathrm{2}\:+\frac{\pi}{\mathrm{2}}\:−\mathrm{2} \\ $$$${lim}_{{n}−>\propto} {ln}\left({V}_{{n}} \right)=\:{ln}\mathrm{2}\:+\frac{\pi}{\mathrm{2}}\:−\mathrm{2} \\ $$$$\Rightarrow\:{lim}_{{n}−>\propto^{} } \:{V}_{{n}} \:=\:\mathrm{2}\:{e}^{\frac{\pi}{\mathrm{2}}−\mathrm{2}} \:\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *