let-give-u-n-k-1-n-1-k-ln-n-1-prove-that-u-n-is-convergent-2-if-lim-n-u-n-prove-the-0-lt-lt-1-

Tinku Tara June 4, 2023 Relation and Functions 0 Comments

Question Number 31417 by abdo imad last updated on 08/Mar/18

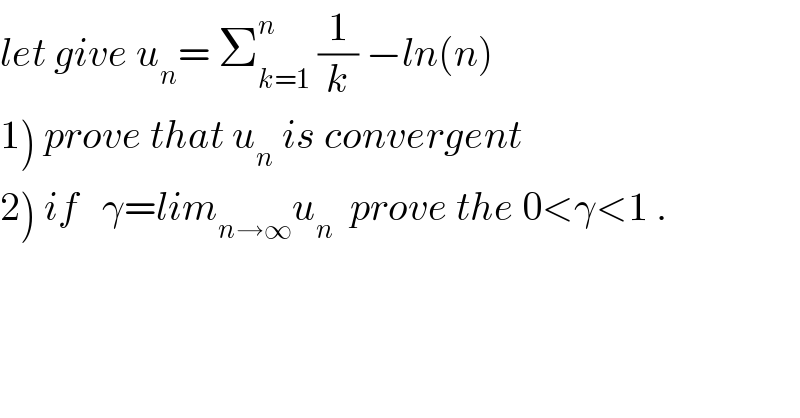
let give u_n = Σ_(k=1) ^n (1/k) −ln(n) 1) prove that u_n is convergent 2) if γ=lim_(n→∞) u_n prove the 0<γ<1 .

$${let}\:{give}\:{u}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:−{ln}\left({n}\right) \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:{u}_{{n}} \:{is}\:{convergent}\: \\ $$$$\left.\mathrm{2}\right)\:{if}\:\:\:\gamma={lim}_{{n}\rightarrow\infty} {u}_{{n}} \:\:{prove}\:{the}\:\mathrm{0}<\gamma<\mathrm{1}\:. \\ $$

Facebook Tweet Pin

let-give-u-n-k-1-n-1-k-ln-n-1-prove-that-u-n-is-convergent-2-if-lim-n-u-n-prove-the-0-lt-lt-1-

Leave a Reply Cancel reply