Question Number 33590 by abdo imad last updated on 19/Apr/18
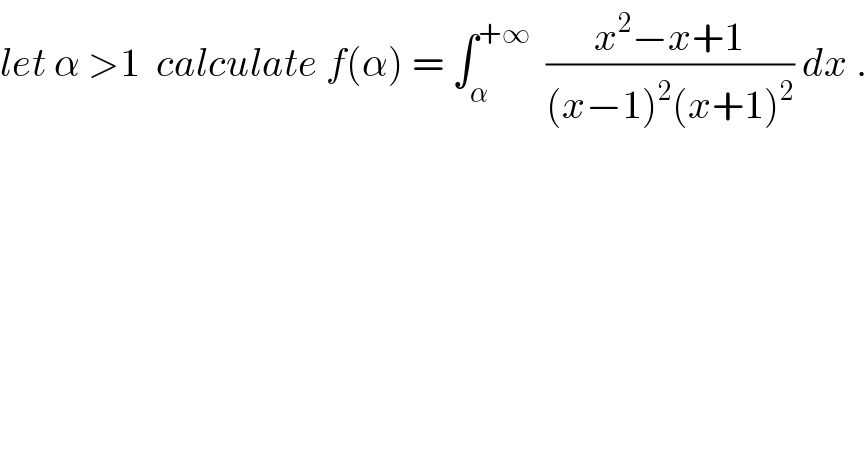
$${let}\:\alpha\:>\mathrm{1}\:\:{calculate}\:{f}\left(\alpha\right)\:=\:\int_{\alpha} ^{+\infty} \:\:\frac{{x}^{\mathrm{2}} −{x}+\mathrm{1}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:{dx}\:. \\ $$
Commented by abdo imad last updated on 22/Apr/18
![we have f(α) = ∫_α ^(+∞) ((x^2 −2x+1 +x)/((x−1)^2 (x+1)^2 ))dx =∫_α ^(+∞) (((x−1)^2 +x)/((x−1)^2 (x+1)^2 ))dx = ∫_α ^(+∞) (dx/((x+1)^2 )) +∫_α ^(+∞) (x/((x−1)^2 (x+1)^2 ))dx =[((−1)/(x+1))]_α ^(+∞) +∫_α ^(+∞) ((xdx)/((x−1)^2 (x+1)^2 )) =(1/(α+1)) + I let findI F(x) = (x/((x−1)^2 (x+1)^2 ))=(a/(x−1)) +(b/((x−1)^2 )) +(c/(x+1)) +(d/((x+1)^2 )) b= lim_(x→1) (x−1)^2 F(x) =(1/4) d =lim_(x→−1) (x+1)^2 F(x)=((−1)/4) ⇒ F(x)=(a/(x−1)) +(1/(4(x−1)^2 )) +(c/(x+1)) +((−1)/(4(x+1)^2 )) F(0) =0 =−a +(1/4) +c −(1/4) ⇒c=a ⇒ F(x) =(a/(x−1)) +(1/(4(x−1)^2 )) +(a/(x+1)) −(1/(4(x+1)^2 )) F(2)= (2/9) = a +(1/4) +(a/3) −(1/(36)) ⇒2=9a +(9/4) +3 −(1/4) ⇒ 2 =9a +5 ⇒9a =−3 ⇒ a=−(1/3) ⇒ F(x)=−(1/(3(x−1))) +(1/(4(x−1)^2 )) −(1/(3(x+1))) −(1/(4(x+1)^2 )) I =∫_α ^(+∞) ( (1/(3(1−x))) −(1/(3(1+x))))dx +(1/4) ∫_α ^(+∞) (dx/((x−1)^2 )) −(1/4) ∫_α ^(+∞) (dx/((x+1)^2 )) =[(1/3)ln∣((1−x)/(1+x))∣]_α ^(+∞) −(1/4)[ (1/(x−1))]_α ^(+∞) +(1/4)[ (1/(x+1))]_α ^(+∞) =(1/3)ln∣((1−α)/(1+α))∣ +(1/(4(α−1))) −(1/(4(α+1))) ⇒ f(α) = (3/(4(α+1))) +(1/3)ln∣((1−α)/(1+α))∣ +(1/(4(α−1))) .](https://www.tinkutara.com/question/Q33712.png)
$${we}\:{have}\:{f}\left(\alpha\right)\:=\:\int_{\alpha} ^{+\infty} \:\frac{{x}^{\mathrm{2}} \:−\mathrm{2}{x}+\mathrm{1}\:+{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\int_{\alpha} ^{+\infty} \:\frac{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \:+{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx}\:=\:\int_{\alpha} ^{+\infty} \:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:\:+\int_{\alpha} ^{+\infty} \:\:\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }{dx} \\ $$$$=\left[\frac{−\mathrm{1}}{{x}+\mathrm{1}}\right]_{\alpha} ^{+\infty} \:+\int_{\alpha} ^{+\infty} \:\:\:\:\frac{{xdx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\alpha+\mathrm{1}}\:+\:{I}\:{let}\:{findI} \\ $$$${F}\left({x}\right)\:=\:\frac{{x}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{{b}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{c}}{{x}+\mathrm{1}}\:+\frac{{d}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${b}=\:{lim}_{{x}\rightarrow\mathrm{1}} \left({x}−\mathrm{1}\right)^{\mathrm{2}} {F}\left({x}\right)\:=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${d}\:={lim}_{{x}\rightarrow−\mathrm{1}} \left({x}+\mathrm{1}\right)^{\mathrm{2}} {F}\left({x}\right)=\frac{−\mathrm{1}}{\mathrm{4}}\:\Rightarrow \\ $$$${F}\left({x}\right)=\frac{{a}}{{x}−\mathrm{1}}\:\:+\frac{\mathrm{1}}{\mathrm{4}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{{c}}{{x}+\mathrm{1}}\:\:+\frac{−\mathrm{1}}{\mathrm{4}\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)\:=\mathrm{0}\:=−{a}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+{c}\:−\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow{c}={a}\:\Rightarrow \\ $$$${F}\left({x}\right)\:=\frac{{a}}{{x}−\mathrm{1}}\:+\frac{\mathrm{1}}{\mathrm{4}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:\:+\frac{{a}}{{x}+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{4}\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{2}\right)=\:\frac{\mathrm{2}}{\mathrm{9}}\:=\:{a}\:+\frac{\mathrm{1}}{\mathrm{4}}\:+\frac{{a}}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{36}}\:\Rightarrow\mathrm{2}=\mathrm{9}{a}\:+\frac{\mathrm{9}}{\mathrm{4}}\:+\mathrm{3}\:−\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\Rightarrow\:\mathrm{2}\:=\mathrm{9}{a}\:+\mathrm{5}\:\Rightarrow\mathrm{9}{a}\:=−\mathrm{3}\:\Rightarrow\:{a}=−\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow \\ $$$${F}\left({x}\right)=−\frac{\mathrm{1}}{\mathrm{3}\left({x}−\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{4}\left({x}−\mathrm{1}\right)^{\mathrm{2}} }\:−\frac{\mathrm{1}}{\mathrm{3}\left({x}+\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{4}\left({x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$${I}\:=\int_{\alpha} ^{+\infty} \:\left(\:\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}−{x}\right)}\:−\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{1}+{x}\right)}\right){dx}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\alpha} ^{+\infty} \:\frac{{dx}}{\left({x}−\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$−\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\alpha} ^{+\infty} \:\:\frac{{dx}}{\left({x}+\mathrm{1}\right)^{\mathrm{2}} }\:=\left[\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}\mid\right]_{\alpha} ^{+\infty} \:−\frac{\mathrm{1}}{\mathrm{4}}\left[\:\frac{\mathrm{1}}{{x}−\mathrm{1}}\right]_{\alpha} ^{+\infty} \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}\left[\:\frac{\mathrm{1}}{{x}+\mathrm{1}}\right]_{\alpha} ^{+\infty} \:=\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid\frac{\mathrm{1}−\alpha}{\mathrm{1}+\alpha}\mid\:+\frac{\mathrm{1}}{\mathrm{4}\left(\alpha−\mathrm{1}\right)}\:−\frac{\mathrm{1}}{\mathrm{4}\left(\alpha+\mathrm{1}\right)}\:\Rightarrow \\ $$$${f}\left(\alpha\right)\:=\:\frac{\mathrm{3}}{\mathrm{4}\left(\alpha+\mathrm{1}\right)}\:+\frac{\mathrm{1}}{\mathrm{3}}{ln}\mid\frac{\mathrm{1}−\alpha}{\mathrm{1}+\alpha}\mid\:+\frac{\mathrm{1}}{\mathrm{4}\left(\alpha−\mathrm{1}\right)}\:. \\ $$
