Menu Close

let-I-0-cos-4-t-e-2t-dt-and-J-0-sin-4-t-e-2t-dt-1-calculate-I-J-and-I-J-2-find-the-values-of-I-and-J-

Tinku Tara 0 Comments
Pin




Question Number 44308 by abdo.msup.com last updated on 26/Sep/18
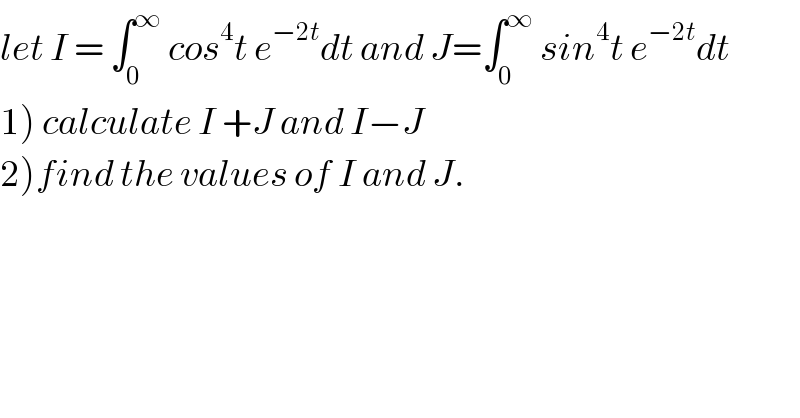
let I = ∫_0 ^∞ cos^4 t e^(−2t) dt and J=∫_0 ^∞ sin^4 t e^(−2t) dt 1) calculate I +J and I−J 2)find the values of I and J.
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\infty} \:{cos}^{\mathrm{4}} {t}\:{e}^{−\mathrm{2}{t}} {dt}\:{and}\:{J}=\int_{\mathrm{0}} ^{\infty} \:{sin}^{\mathrm{4}} {t}\:{e}^{−\mathrm{2}{t}} {dt} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{I}\:+{J}\:{and}\:{I}−{J} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{values}\:{of}\:{I}\:{and}\:{J}. \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 27/Sep/18
Commented by maxmathsup by imad last updated on 28/Sep/18
1) we have I +J = ∫_0 ^∞ (cos^4 t +sin^4 t)e^(−2t) dt =∫_0 ^∞ { (cos^2 t +sin^2 t)^2 −2cos^2 t sin^2 t}e^(−2t) dt = ∫_0 ^∞ {1−(1/2)sin^2 (2t)}e^(−2t) dt = ∫_0 ^∞ e^(−2t) dt −(1/2) ∫_0 ^∞ ( ((1−cos(2t))/2))e^(−2t) dt =[−(1/2)e^(−2t) ]_0 ^(+∞) −(1/4) ∫_0 ^∞ e^(−2t) dt +(1/4) ∫_0 ^∞ e^(−2t) cos(2t)dt =(1/2) +(1/8)[ e^(−2t) ]_0 ^(+∞) +(1/4)∫_0 ^∞ e^(−2t) cos(2t)dt=(3/8) +(1/4) Re(∫_0 ^∞ e^(−2t+i2t) dt) but ∫_0 ^∞ e^((−2+2i)t) dt =[ (1/(−2+2i)) e^((−2+2i)t) ]_0 ^(+∞) =((−1)/(−2+2i)) =(1/(2−2i)) = ((2+2i)/8) =((1+i)/4) ⇒ I +J =(3/8) +(1/(16)) =(7/(16)) also we have I−J =∫_0 ^∞ (cos^4 t −sin^4 t)e^(−2t) dt =∫_0 ^∞ (cos^2 t −sin^2 t)e^(−2t) dt =∫_0 ^∞ e^(−2t) cos(2t)dt =Re( ∫_0 ^∞ e^((−2+2i)t) dt)=(1/4) 2) we have I +J =(7/(16)) and I−J =(1/4) ⇒ 2I =(7/(16)) +(1/4) =((11)/(16)) ⇒I =((11)/(32)) and J =(7/(16)) −((11)/(32)) =((14−11)/(32)) =(3/(32)) .
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{I}\:+{J}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\left({cos}^{\mathrm{4}} {t}\:+{sin}^{\mathrm{4}} {t}\right){e}^{−\mathrm{2}{t}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\left\{\:\left({cos}^{\mathrm{2}} {t}\:+{sin}^{\mathrm{2}} {t}\right)^{\mathrm{2}} −\mathrm{2}{cos}^{\mathrm{2}} {t}\:{sin}^{\mathrm{2}} {t}\right\}{e}^{−\mathrm{2}{t}} {dt} \\ $$$$=\:\int_{\mathrm{0}} ^{\infty} \:\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}}{sin}^{\mathrm{2}} \left(\mathrm{2}{t}\right)\right\}{e}^{−\mathrm{2}{t}} {dt}\:=\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{t}} {dt}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} \left(\:\frac{\mathrm{1}−{cos}\left(\mathrm{2}{t}\right)}{\mathrm{2}}\right){e}^{−\mathrm{2}{t}} {dt} \\ $$$$=\left[−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−\mathrm{2}{t}} \right]_{\mathrm{0}} ^{+\infty} \:−\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{t}} {dt}\:+\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{t}} \:{cos}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{8}}\left[\:{e}^{−\mathrm{2}{t}} \right]_{\mathrm{0}} ^{+\infty} \:+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \:\:{e}^{−\mathrm{2}{t}} \:{cos}\left(\mathrm{2}{t}\right){dt}=\frac{\mathrm{3}}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:{Re}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{t}+{i}\mathrm{2}{t}} {dt}\right) \\ $$$${but}\:\:\int_{\mathrm{0}} ^{\infty} \:\:\:{e}^{\left(−\mathrm{2}+\mathrm{2}{i}\right){t}} {dt}\:=\left[\:\frac{\mathrm{1}}{−\mathrm{2}+\mathrm{2}{i}}\:{e}^{\left(−\mathrm{2}+\mathrm{2}{i}\right){t}} \right]_{\mathrm{0}} ^{+\infty} \:=\frac{−\mathrm{1}}{−\mathrm{2}+\mathrm{2}{i}}\:=\frac{\mathrm{1}}{\mathrm{2}−\mathrm{2}{i}} \\ $$$$=\:\frac{\mathrm{2}+\mathrm{2}{i}}{\mathrm{8}}\:=\frac{\mathrm{1}+{i}}{\mathrm{4}}\:\Rightarrow\:{I}\:+{J}\:=\frac{\mathrm{3}}{\mathrm{8}}\:+\frac{\mathrm{1}}{\mathrm{16}}\:=\frac{\mathrm{7}}{\mathrm{16}}\:\:{also}\:{we}\:{have} \\ $$$${I}−{J}\:=\int_{\mathrm{0}} ^{\infty} \:\:\left({cos}^{\mathrm{4}} {t}\:−{sin}^{\mathrm{4}} {t}\right){e}^{−\mathrm{2}{t}} {dt}\:=\int_{\mathrm{0}} ^{\infty} \:\left({cos}^{\mathrm{2}} {t}\:−{sin}^{\mathrm{2}} {t}\right){e}^{−\mathrm{2}{t}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\mathrm{2}{t}} \:{cos}\left(\mathrm{2}{t}\right){dt}\:={Re}\left(\:\int_{\mathrm{0}} ^{\infty} \:\:{e}^{\left(−\mathrm{2}+\mathrm{2}{i}\right){t}} {dt}\right)=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{I}\:+{J}\:=\frac{\mathrm{7}}{\mathrm{16}}\:{and}\:{I}−{J}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\Rightarrow\:\mathrm{2}{I}\:=\frac{\mathrm{7}}{\mathrm{16}}\:+\frac{\mathrm{1}}{\mathrm{4}}\:=\frac{\mathrm{11}}{\mathrm{16}}\:\Rightarrow{I}\:=\frac{\mathrm{11}}{\mathrm{32}} \\ $$$${and}\:{J}\:=\frac{\mathrm{7}}{\mathrm{16}}\:−\frac{\mathrm{11}}{\mathrm{32}}\:=\frac{\mathrm{14}−\mathrm{11}}{\mathrm{32}}\:=\frac{\mathrm{3}}{\mathrm{32}}\:. \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Sep/18
I+J=∫_0 ^∞ e^(−2t) (cos^4 t+sin^4 t)dt =∫_0 ^∞ e^(−2t) {(cos^2 t+sin^2 t)^2 −2sin^2 tcos^2 t}dt =∫_0 ^∞ e^(−2t) {1−((sin^2 2t)/2)}dt =∫_0 ^∞ e^(−2t) {1−((1−cos4t)/4)} =∫_0 ^∞ e^(−2t) (((4−1+cos4t)/4)} =(3/4)∫_0 ^∞ e^(−2t) dt+(1/4)∫_0 ^∞ e^(−2t) cos4t dt formula ∫e^(ax) cosbx dx=((e^(ax) (acosbx+bsinbx))/(a^2 +b^2 )) =(3/4)∣(e^(−2t) /(−2))∣_0 ^∞ +(1/4)∣((e^(−2t) (−2cos4t+4sin4t))/((−2)^2 +(4)^2 ))∣_0 ^∞ I−J=∫_0 ^∞ e^(−2t) (cos^4 t−sin^4 t)dt =∫_0 ^∞ e^(−2t) cos2t dt =∣((e^(−2t) (−2cos2t+2sin2t)/((−2)^2 +(4^2 )))∣_0 ^∞ pls check upper limit of the interval...
$${I}+{J}=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} \left({cos}^{\mathrm{4}} {t}+{sin}^{\mathrm{4}} {t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} \left\{\left({cos}^{\mathrm{2}} {t}+{sin}^{\mathrm{2}} {t}\right)^{\mathrm{2}} −\mathrm{2}{sin}^{\mathrm{2}} {tcos}^{\mathrm{2}} {t}\right\}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} \left\{\mathrm{1}−\frac{{sin}^{\mathrm{2}} \mathrm{2}{t}}{\mathrm{2}}\right\}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} \left\{\mathrm{1}−\frac{\mathrm{1}−{cos}\mathrm{4}{t}}{\mathrm{4}}\right\} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} \left(\frac{\mathrm{4}−\mathrm{1}+{cos}\mathrm{4}{t}}{\mathrm{4}}\right\} \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} {dt}+\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} {cos}\mathrm{4}{t}\:{dt} \\ $$$${formula}\:\int{e}^{{ax}} {cosbx}\:{dx}=\frac{{e}^{{ax}} \left({acosbx}+{bsinbx}\right)}{{a}^{\mathrm{2}} +{b}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\mid\frac{{e}^{−\mathrm{2}{t}} }{−\mathrm{2}}\mid_{\mathrm{0}} ^{\infty} +\frac{\mathrm{1}}{\mathrm{4}}\mid\frac{{e}^{−\mathrm{2}{t}} \left(−\mathrm{2}{cos}\mathrm{4}{t}+\mathrm{4}{sin}\mathrm{4}{t}\right)}{\left(−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{4}\right)^{\mathrm{2}} }\mid_{\mathrm{0}} ^{\infty} \\ $$$${I}−{J}=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} \left({cos}^{\mathrm{4}} {t}−{sin}^{\mathrm{4}} {t}\right){dt} \\ $$$$=\int_{\mathrm{0}} ^{\infty} {e}^{−\mathrm{2}{t}} {cos}\mathrm{2}{t}\:{dt} \\ $$$$=\mid\frac{{e}^{−\mathrm{2}{t}} \left(−\mathrm{2}{cos}\mathrm{2}{t}+\mathrm{2}{sin}\mathrm{2}{t}\right.}{\left(−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{4}^{\mathrm{2}} \right)}\mid_{\mathrm{0}} ^{\infty} \\ $$$${pls}\:{check}\:{upper}\:{limit}\:{of}\:{the}\:{interval}… \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *