Menu Close

let-I-0-pi-2-cos-6-x-dx-and-J-0-pi-2-sin-6-xdx-1-cslculate-I-J-and-I-J-2-find-the-value-of-I-and-J-

Tinku Tara 0 Comments
Pin




Question Number 41053 by turbo msup by abdo last updated on 01/Aug/18
let I = ∫_0 ^(π/2) cos^6 x dx and J = ∫_0 ^(π/2) sin^6 xdx 1)cslculate I +J and I−J 2)find the value of I and J
$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{6}} {x}\:{dx}\:{and} \\ $$$${J}\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sin}^{\mathrm{6}} {xdx} \\ $$$$\left.\mathrm{1}\right){cslculate}\:{I}\:+{J}\:\:{and}\:{I}−{J} \\ $$$$\left.\mathrm{2}\right){find}\:{the}\:{value}\:{of}\:{I}\:{and}\:{J} \\ $$
Commented by prof Abdo imad last updated on 01/Aug/18
2) we have I +J =((5π)/(16)) and I−J =0 ⇒ I=J and 2I =((5π)/(16)) ⇒ I =J =((5π)/(32)) .
$$\left.\mathrm{2}\right)\:{we}\:{have}\:{I}\:+{J}\:=\frac{\mathrm{5}\pi}{\mathrm{16}}\:{and}\:{I}−{J}\:=\mathrm{0}\:\Rightarrow \\ $$$${I}={J}\:\:{and}\:\mathrm{2}{I}\:=\frac{\mathrm{5}\pi}{\mathrm{16}}\:\Rightarrow\:{I}\:={J}\:=\frac{\mathrm{5}\pi}{\mathrm{32}}\:. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Aug/18
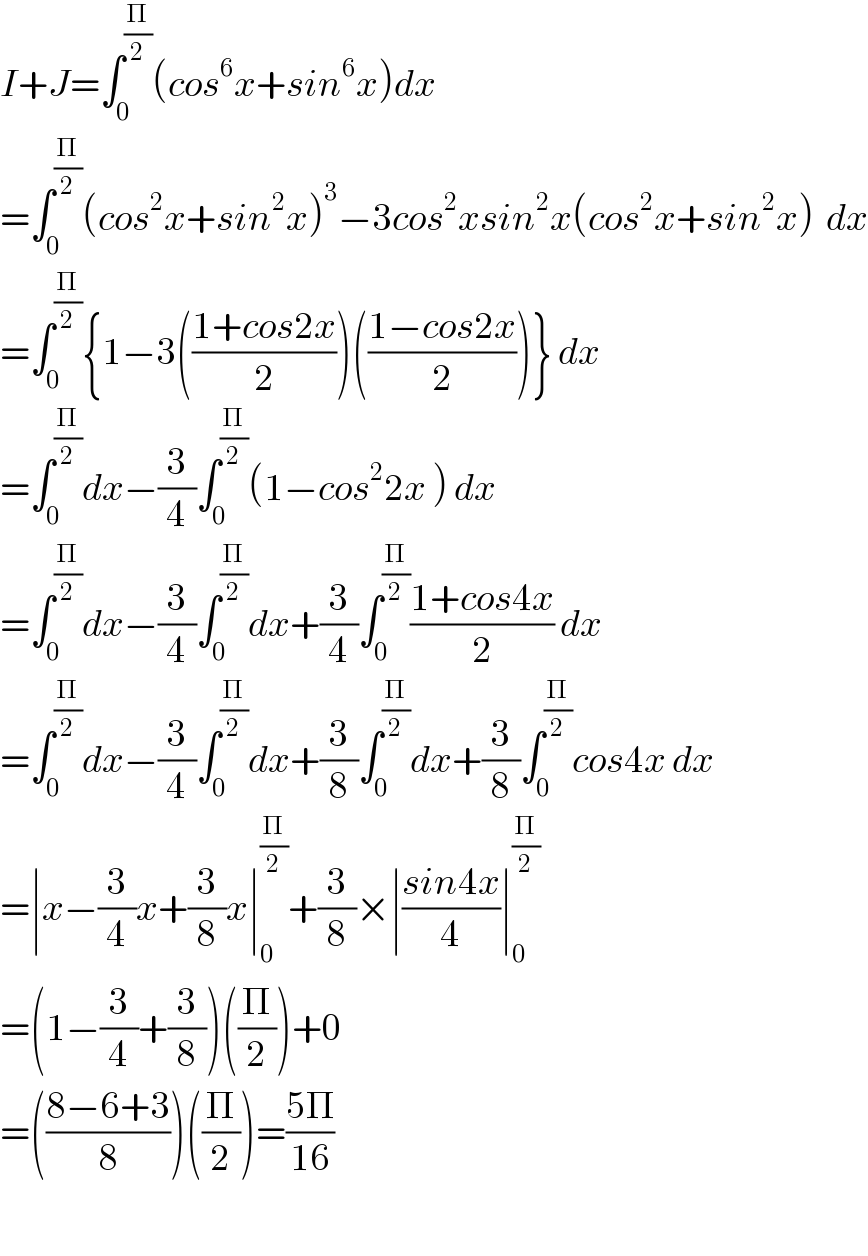
I+J=∫_0 ^(Π/2) (cos^6 x+sin^6 x)dx =∫_0 ^(Π/2) (cos^2 x+sin^2 x)^3 −3cos^2 xsin^2 x(cos^2 x+sin^2 x) dx =∫_0 ^(Π/2) {1−3(((1+cos2x)/2))(((1−cos2x)/2))} dx =∫_0 ^(Π/2) dx−(3/4)∫_0 ^(Π/2) (1−cos^2 2x ) dx =∫_0 ^(Π/2) dx−(3/4)∫_0 ^(Π/2) dx+(3/4)∫_0 ^(Π/2) ((1+cos4x)/2) dx =∫_0 ^(Π/2) dx−(3/4)∫_0 ^(Π/2) dx+(3/8)∫_0 ^(Π/2) dx+(3/8)∫_0 ^(Π/2) cos4x dx =∣x−(3/4)x+(3/8)x∣_0 ^(Π/2) +(3/8)×∣((sin4x)/4)∣_0 ^(Π/2) =(1−(3/4)+(3/8))((Π/2))+0 =(((8−6+3)/8))((Π/2))=((5Π)/(16))
$${I}+{J}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \left({cos}^{\mathrm{6}} {x}+{sin}^{\mathrm{6}} {x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \left({cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} −\mathrm{3}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}\left({cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}\right)\:\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \left\{\mathrm{1}−\mathrm{3}\left(\frac{\mathrm{1}+{cos}\mathrm{2}{x}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}}\right)\right\}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {dx}−\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \left(\mathrm{1}−{cos}^{\mathrm{2}} \mathrm{2}{x}\:\right)\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {dx}−\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {dx}+\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{\mathrm{1}+{cos}\mathrm{4}{x}}{\mathrm{2}}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {dx}−\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {dx}+\frac{\mathrm{3}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {dx}+\frac{\mathrm{3}}{\mathrm{8}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {cos}\mathrm{4}{x}\:{dx} \\ $$$$=\mid{x}−\frac{\mathrm{3}}{\mathrm{4}}{x}+\frac{\mathrm{3}}{\mathrm{8}}{x}\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} +\frac{\mathrm{3}}{\mathrm{8}}×\mid\frac{{sin}\mathrm{4}{x}}{\mathrm{4}}\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{8}}\right)\left(\frac{\Pi}{\mathrm{2}}\right)+\mathrm{0} \\ $$$$=\left(\frac{\mathrm{8}−\mathrm{6}+\mathrm{3}}{\mathrm{8}}\right)\left(\frac{\Pi}{\mathrm{2}}\right)=\frac{\mathrm{5}\Pi}{\mathrm{16}} \\ $$$$ \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 01/Aug/18
I−J=∫_0 ^(Π/2) (cos^6 x−sin^6 x)dx =∫_0 ^(Π/2) (cos^2 x−sin^2 x)^3 +3cos^2 xsin^2 x(cos^2 x−sin^2 x)dx =∫_0 ^(Π/2) cos^3 2x+3(((1+cos2x)/2))(((1−cos2x)/2))(cos2x) dx =∫_0 ^(Π/2) ((cos6x+3cos2x)/4)+(3/4)(1−((1+cos4x)/2))(cos2x) dx =(1/4)∫_0 ^(Π/2) cos6x+(3/4)∫_0 ^(Π/2) cos2x+∫_0 ^(Π/2) ((2−1−cos4x)/2)cos2x dx =0+0+(1/2)∫_0 ^(Π/2) (((1−cos4x)cos2x)/) =(1/2)∫_0 ^(Π/2) (cos2x)−(1/4)∫_0 ^(Π/2) cos6x+cos2x dx =0 ∫_0 ^(Π/2) cos2x dx=∣((sin2x)/2)∣_0 ^(Π/2) =0 ∫_0 ^(Π/2) cos6x=∣((sin6x)/6)∣_0 ^(Π/2) =((sin3Π−sin0)/6)=0
$${I}−{J}=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \left({cos}^{\mathrm{6}} {x}−{sin}^{\mathrm{6}} {x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \:\left({cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} +\mathrm{3}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}\left({cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {cos}^{\mathrm{3}} \mathrm{2}{x}+\mathrm{3}\left(\frac{\mathrm{1}+{cos}\mathrm{2}{x}}{\mathrm{2}}\right)\left(\frac{\mathrm{1}−{cos}\mathrm{2}{x}}{\mathrm{2}}\right)\left({cos}\mathrm{2}{x}\right)\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{{cos}\mathrm{6}{x}+\mathrm{3}{cos}\mathrm{2}{x}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}\left(\mathrm{1}−\frac{\mathrm{1}+{cos}\mathrm{4}{x}}{\mathrm{2}}\right)\left({cos}\mathrm{2}{x}\right)\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {cos}\mathrm{6}{x}+\frac{\mathrm{3}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {cos}\mathrm{2}{x}+\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{\mathrm{2}−\mathrm{1}−{cos}\mathrm{4}{x}}{\mathrm{2}}{cos}\mathrm{2}{x}\:{dx} \\ $$$$=\mathrm{0}+\mathrm{0}+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \frac{\left(\mathrm{1}−{cos}\mathrm{4}{x}\right){cos}\mathrm{2}{x}}{} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} \left({cos}\mathrm{2}{x}\right)−\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {cos}\mathrm{6}{x}+{cos}\mathrm{2}{x}\:\:{dx} \\ $$$$=\mathrm{0} \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {cos}\mathrm{2}{x}\:{dx}=\mid\frac{{sin}\mathrm{2}{x}}{\mathrm{2}}\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} =\mathrm{0} \\ $$$$\int_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} {cos}\mathrm{6}{x}=\mid\frac{{sin}\mathrm{6}{x}}{\mathrm{6}}\mid_{\mathrm{0}} ^{\frac{\Pi}{\mathrm{2}}} =\frac{{sin}\mathrm{3}\Pi−{sin}\mathrm{0}}{\mathrm{6}}=\mathrm{0} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Aug/18
so I=((5Π)/(32)) J=((5Π)/(32))
$${so}\:{I}=\frac{\mathrm{5}\Pi}{\mathrm{32}}\:\:\:{J}=\frac{\mathrm{5}\Pi}{\mathrm{32}} \\ $$
Commented by prof Abdo imad last updated on 01/Aug/18
your answer is correct sir Tanmay thanks.
$${your}\:{answer}\:{is}\:{correct}\:{sir}\:{Tanmay}\:{thanks}. \\ $$
Answered by prof Abdo imad last updated on 01/Aug/18
1) we use the formulae a^(3 ) +b^3 =(a+b)^3 −3ab and a^3 −b^3 =(a−b)^3 +3ab I +J =∫_0 ^(π/2) ((cos^2 x)^3 +(sin^2 x)^3 )dx =∫_0 ^(π/2) (cos^2 x+sin^2 x)^3 −3cos^2 x sin^2 x)dx =(π/2) −3 ∫_0 ^(π/2) ((1+cos(2x))/2)((1−cos(2x))/2)dx =(π/2) −(3/4) ∫_0 ^(π/2) (1−cos^2 (2x))dx =(π/2)−(3/4) ∫_0 ^(π/2) (1−((1+cos(4x))/2))dx =(π/2) −(3/8) ∫_0 ^(π/2) (1−cos(4x))dx =(π/2) −((3π)/(16)) +(3/8) ∫_0 ^(π/2) cos(4x)dx =((5π)/(16)) +(3/(64))[sin(4x)]_0 ^(π/2) =((5π)/(16))
$$\left.\mathrm{1}\right)\:{we}\:{use}\:{the}\:{formulae}\:{a}^{\mathrm{3}\:} +{b}^{\mathrm{3}} =\left({a}+{b}\right)^{\mathrm{3}} −\mathrm{3}{ab} \\ $$$${and}\:{a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}−{b}\right)^{\mathrm{3}} \:+\mathrm{3}{ab} \\ $$$${I}\:+{J}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\left({cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \:+\left({sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \right){dx} \\ $$$$\left.=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({cos}^{\mathrm{2}} {x}+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} −\mathrm{3}{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}\right){dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\mathrm{3}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{\mathrm{1}+{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}{dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{3}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−{cos}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\right){dx} \\ $$$$=\frac{\pi}{\mathrm{2}}−\frac{\mathrm{3}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{1}−\frac{\mathrm{1}+{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\right){dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{3}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)\right){dx} \\ $$$$=\frac{\pi}{\mathrm{2}}\:−\frac{\mathrm{3}\pi}{\mathrm{16}}\:+\frac{\mathrm{3}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{4}{x}\right){dx} \\ $$$$=\frac{\mathrm{5}\pi}{\mathrm{16}}\:+\frac{\mathrm{3}}{\mathrm{64}}\left[{sin}\left(\mathrm{4}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:=\frac{\mathrm{5}\pi}{\mathrm{16}} \\ $$
Commented by tanmay.chaudhury50@gmail.com last updated on 01/Aug/18
a^3 +b^3 =(a+b)^3 −3ab(a+b) or a^3 +b^3 =(a+b)(a^2 −ab+b^2 ) a^3 −b^3 =(a−b)^3 +3ab(a−b) or a^3 −b^3 =(a−b)(a^2 +ab+b^2 )
$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\left({a}+{b}\right)^{\mathrm{3}} −\mathrm{3}{ab}\left({a}+{b}\right) \\ $$$$\:\:\:{or}\:{a}^{\mathrm{3}} +{b}^{\mathrm{3}} =\left({a}+{b}\right)\left({a}^{\mathrm{2}} −{ab}+{b}^{\mathrm{2}} \right) \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}−{b}\right)^{\mathrm{3}} +\mathrm{3}{ab}\left({a}−{b}\right) \\ $$$${or}\:{a}^{\mathrm{3}} −{b}^{\mathrm{3}} =\left({a}−{b}\right)\left({a}^{\mathrm{2}} +{ab}+{b}^{\mathrm{2}} \right) \\ $$
Commented by math khazana by abdo last updated on 01/Aug/18
error at the first line a^3 +b^3 =(a+b)^3 −3ab(a+b) and a^3 −b^3 =(a−b)^3 +3ab(a−b)
$${error}\:{at}\:{the}\:{first}\:{line} \\ $$$${a}^{\mathrm{3}} \:+{b}^{\mathrm{3}} \:=\left({a}+{b}\right)^{\mathrm{3}} −\mathrm{3}{ab}\left({a}+{b}\right)\:{and} \\ $$$${a}^{\mathrm{3}} −{b}^{\mathrm{3}} \:=\left({a}−{b}\right)^{\mathrm{3}} \:+\mathrm{3}{ab}\left({a}−{b}\right) \\ $$
Answered by prof Abdo imad last updated on 01/Aug/18
I−J = ∫_0 ^(π/2) ((cos^2 x)^3 −(sin^2 x)^3 )dx =∫_0 ^(π/2) (cos^2 x−sin^2 x)^3 +3cos^2 x sin^2 x(cos^2 x−sin^2 x)dx =∫_0 ^(π/2) (cos^2 x−sin^2 x){(cos^2 x−sin^2 x)^2 +3cos^2 xsin^2 x}dx =∫_0 ^(π/2) cos(2x)( cos^4 x +sin^4 x +sin^2 x cos^2 x)dx =∫_0 ^(π/2) cos(2x){ (cos^2 x +sin^2 x)^2 −cos^2 xsin^2 x}dx =∫_0 ^(π/2) cos(2x){1−(1/4)sin^2 (2x)}dx =(1/4) ∫_0 ^(π/2) cos(2x)(4−((1−cos(4x))/2))dx =(1/8) ∫_0 ^(π/2) cos(2x)(7−cos(4x))dx =(7/8) [(1/2)sin(2x)]_0 ^(π/2) −(1/8) ∫_0 ^(π/2) cos(2x)cos(4x) =−(1/(16)) ∫_0 ^(π/2) {cos(6x)+cos(2x))dx =0 ⇒I−J=0
$${I}−{J}\:\:=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\left({cos}^{\mathrm{2}} {x}\right)^{\mathrm{3}} −\left({sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\right)^{\mathrm{3}} \:+\mathrm{3}{cos}^{\mathrm{2}} {x}\:{sin}^{\mathrm{2}} {x}\left({cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left({cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\right)\left\{\left({cos}^{\mathrm{2}} {x}−{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \:+\mathrm{3}{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}\right\}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}{x}\right)\left(\:{cos}^{\mathrm{4}} {x}\:+{sin}^{\mathrm{4}} {x}\:\:+{sin}^{\mathrm{2}} {x}\:{cos}^{\mathrm{2}} {x}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {cos}\left(\mathrm{2}{x}\right)\left\{\:\left({cos}^{\mathrm{2}} {x}\:+{sin}^{\mathrm{2}} {x}\right)^{\mathrm{2}} \:−{cos}^{\mathrm{2}} {xsin}^{\mathrm{2}} {x}\right\}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}{x}\right)\left\{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}{sin}^{\mathrm{2}} \left(\mathrm{2}{x}\right)\right\}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}{x}\right)\left(\mathrm{4}−\frac{\mathrm{1}−{cos}\left(\mathrm{4}{x}\right)}{\mathrm{2}}\right){dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}{x}\right)\left(\mathrm{7}−{cos}\left(\mathrm{4}{x}\right)\right){dx} \\ $$$$=\frac{\mathrm{7}}{\mathrm{8}}\:\left[\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}{x}\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:−\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}\left(\mathrm{2}{x}\right){cos}\left(\mathrm{4}{x}\right) \\ $$$$=−\frac{\mathrm{1}}{\mathrm{16}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left\{{cos}\left(\mathrm{6}{x}\right)+{cos}\left(\mathrm{2}{x}\right)\right){dx}\:=\mathrm{0}\:\Rightarrow{I}−{J}=\mathrm{0} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *