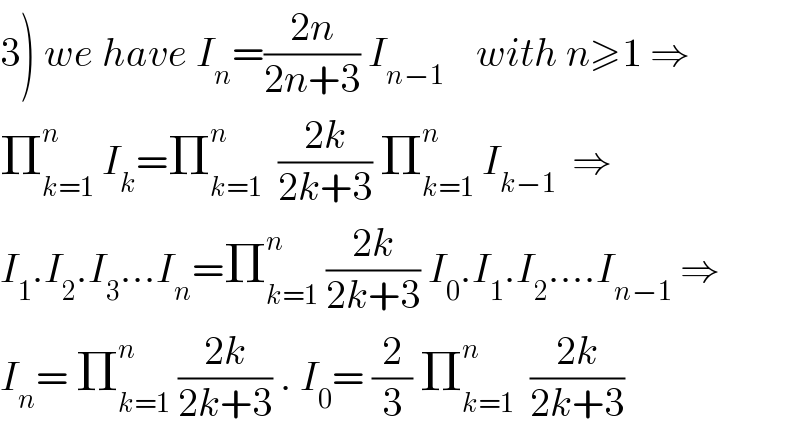Question Number 40139 by maxmathsup by imad last updated on 16/Jul/18
$${let}\:\:{I}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:{x}^{{n}} \sqrt{\mathrm{1}−{x}}\:{dx} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{I}_{\mathrm{0}} \:\:{and}\:{I}_{\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:{prove}\:{that}\:\:\forall{n}\in\:{N}^{\bigstar} \:\:\:\:\left(\mathrm{3}+\mathrm{2}{n}\right)\:{I}_{{n}} =\mathrm{2}{n}\:{I}_{{n}−\mathrm{1}} \\ $$$$\left.\mathrm{3}\right)\:{find}\:{I}_{{n}} \:\:{interms}\:{of}\:{n} \\ $$
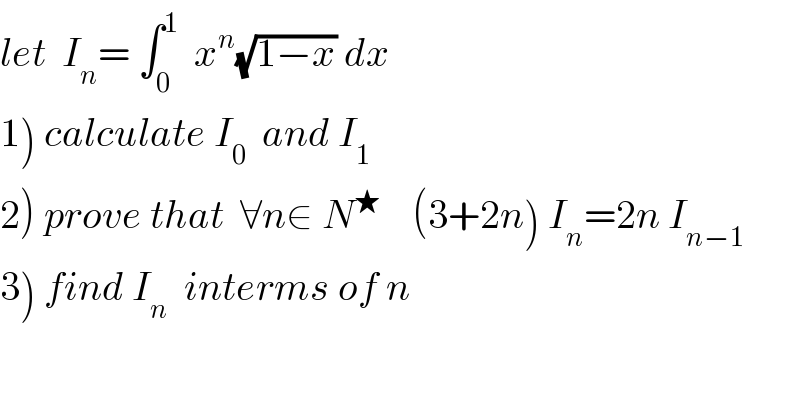
Commented by prof Abdo imad last updated on 20/Jul/18
![1) I_0 =∫_0 ^1 (√(1−x))dx =_(x=sin^2 t) ∫_0 ^(π/2) cost 2sint cost?dt =2 ∫_0 ^(π/2) sint cos^2 t dt =2[−(1/3) cos^3 t]_0 ^(π/2) =−(2/3){0−1}=(2/3) I_1 = ∫_0 ^1 x(√(1−x))dx =_((√(1−x))=t) −∫_0 ^1 (1−t^2 )t(−2tdt) =2 ∫_0 ^1 t^2 (1−t^2 )dt =2 ∫_0 ^1 (t^2 −t^4 )dt =2 [(t^3 /3) −(t^5 /5)]_0 ^1 =2{(1/3) −(1/5)}=2(2/(15)) =(4/(15))](https://www.tinkutara.com/question/Q40358.png)
$$\left.\mathrm{1}\right)\:{I}_{\mathrm{0}} =\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}−{x}}{dx}\:\:=_{{x}={sin}^{\mathrm{2}} {t}} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{cost}\:\mathrm{2}{sint}\:{cost}?{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{sint}\:{cos}^{\mathrm{2}} {t}\:{dt}\:=\mathrm{2}\left[−\frac{\mathrm{1}}{\mathrm{3}}\:{cos}^{\mathrm{3}} {t}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=−\frac{\mathrm{2}}{\mathrm{3}}\left\{\mathrm{0}−\mathrm{1}\right\}=\frac{\mathrm{2}}{\mathrm{3}} \\ $$$${I}_{\mathrm{1}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}\sqrt{\mathrm{1}−{x}}{dx}\:=_{\sqrt{\mathrm{1}−{x}}={t}} \:\:\:\:−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right){t}\left(−\mathrm{2}{tdt}\right) \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right){dt}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({t}^{\mathrm{2}} \:−{t}^{\mathrm{4}} \right){dt} \\ $$$$=\mathrm{2}\:\left[\frac{{t}^{\mathrm{3}} }{\mathrm{3}}\:−\frac{{t}^{\mathrm{5}} }{\mathrm{5}}\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\mathrm{2}\left\{\frac{\mathrm{1}}{\mathrm{3}}\:−\frac{\mathrm{1}}{\mathrm{5}}\right\}=\mathrm{2}\frac{\mathrm{2}}{\mathrm{15}}\:=\frac{\mathrm{4}}{\mathrm{15}} \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 24/Jul/18
![2) changement (√(1−x))=t give 1−x=t^2 I_n = ∫_0 ^1 (1−t^2 )^n t 2tdt = ∫_0 ^1 2t^2 (1−t^2 )^n dt =_(t=sinα) ∫_0 ^(π/2) 2sin^2 α cos^(2n) α cosα dα = ∫_0 ^(π/2) 2sin^2 αcos^(2n) α dα by parts u^′ =sinα cos^(2n) α and v=2sinα I_n = [−(1/(2n+1)) cos^(2n+1) α 2sinα]_0 ^(π/2) −∫_0 ^(π/2) −(1/(2n+1))cos^(2n+1) α .2cosα dα =(2/(2n+1)) ∫_0 ^(π/2) cos^(2n+2) α dα = (2/(2n+1)) ∫_0 ^(π/2) (1 −sin^2 α)cos^(2n) α dα = (2/(2n+1)) ∫_0 ^(π/2) cos^(2n) α dα −(1/(2n+1)) ∫_0 ^(π/2) 2sin^2 α cos^(2n) α dα =(2/(2n+1)) ∫_0 ^(π/2) (1−sin^2 α)cos^(2(n−1)) α dα −(1/(2n+1)) I_n ⇒ (1+(1/(2n+1))) I_n = (2/(2n+1)) ∫_0 ^(π/2) cos^(2(n−1)) α dα −(1/(2n+1)) I_(n−1) ⇒ ((2n+2)/(2n+1)) I_n = (2/(2n+1)) ∫_0 ^(π/2) cos^(2(n−1)) α dα −(1/(2n+1)) I_(n−1) ...be continued...](https://www.tinkutara.com/question/Q40611.png)
$$\left.\mathrm{2}\right)\:{changement}\:\sqrt{\mathrm{1}−{x}}={t}\:{give}\:\mathrm{1}−{x}={t}^{\mathrm{2}} \\ $$$${I}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{{n}} {t}\:\:\mathrm{2}{tdt}\:\:=\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}{t}^{\mathrm{2}} \left(\mathrm{1}−{t}^{\mathrm{2}} \right)^{{n}} \:{dt} \\ $$$$=_{{t}={sin}\alpha} \:\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{2}{sin}^{\mathrm{2}} \alpha\:{cos}^{\mathrm{2}{n}} \alpha\:{cos}\alpha\:{d}\alpha \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{2}{sin}^{\mathrm{2}} \alpha{cos}^{\mathrm{2}{n}} \alpha\:{d}\alpha\:\:{by}\:{parts}\:\:{u}^{'} \:={sin}\alpha\:{cos}^{\mathrm{2}{n}} \alpha\:\:{and}\:{v}=\mathrm{2}{sin}\alpha \\ $$$${I}_{{n}} =\:\left[−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{cos}^{\mathrm{2}{n}+\mathrm{1}} \alpha\:\mathrm{2}{sin}\alpha\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}{cos}^{\mathrm{2}{n}+\mathrm{1}} \alpha\:.\mathrm{2}{cos}\alpha\:{d}\alpha \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\:{cos}^{\mathrm{2}{n}+\mathrm{2}} \alpha\:{d}\alpha\:=\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\left(\mathrm{1}\:−{sin}^{\mathrm{2}} \alpha\right){cos}^{\mathrm{2}{n}} \alpha\:{d}\alpha \\ $$$$=\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}{n}} \alpha\:{d}\alpha\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{2}{sin}^{\mathrm{2}} \alpha\:{cos}^{\mathrm{2}{n}} \alpha\:{d}\alpha \\ $$$$=\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left(\mathrm{1}−{sin}^{\mathrm{2}} \alpha\right){cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \alpha\:{d}\alpha\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{I}_{{n}} \:\Rightarrow \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\right)\:{I}_{{n}} =\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \alpha\:{d}\alpha\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{I}_{{n}−\mathrm{1}} \:\:\Rightarrow \\ $$$$\frac{\mathrm{2}{n}+\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:{I}_{{n}} =\:\frac{\mathrm{2}}{\mathrm{2}{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{cos}^{\mathrm{2}\left({n}−\mathrm{1}\right)} \alpha\:{d}\alpha\:−\frac{\mathrm{1}}{\mathrm{2}{n}+\mathrm{1}}\:{I}_{{n}−\mathrm{1}} \:\:\:…{be}\:{continued}… \\ $$$$ \\ $$
Commented by maxmathsup by imad last updated on 24/Jul/18
$$\left.\mathrm{3}\right)\:{we}\:{have}\:{I}_{{n}} =\frac{\mathrm{2}{n}}{\mathrm{2}{n}+\mathrm{3}}\:{I}_{{n}−\mathrm{1}} \:\:\:\:{with}\:{n}\geqslant\mathrm{1}\:\Rightarrow \\ $$$$\prod_{{k}=\mathrm{1}} ^{{n}} \:{I}_{{k}} =\prod_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{2}{k}}{\mathrm{2}{k}+\mathrm{3}}\:\prod_{{k}=\mathrm{1}} ^{{n}} \:{I}_{{k}−\mathrm{1}} \:\:\Rightarrow \\ $$$${I}_{\mathrm{1}} .{I}_{\mathrm{2}} .{I}_{\mathrm{3}} …{I}_{{n}} =\prod_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}{k}}{\mathrm{2}{k}+\mathrm{3}}\:{I}_{\mathrm{0}} .{I}_{\mathrm{1}} .{I}_{\mathrm{2}} ….{I}_{{n}−\mathrm{1}} \:\Rightarrow \\ $$$${I}_{{n}} =\:\prod_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{2}{k}}{\mathrm{2}{k}+\mathrm{3}}\:.\:{I}_{\mathrm{0}} =\:\frac{\mathrm{2}}{\mathrm{3}}\:\prod_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{2}{k}}{\mathrm{2}{k}+\mathrm{3}} \\ $$