Question Number 154927 by physicstutes last updated on 23/Sep/21
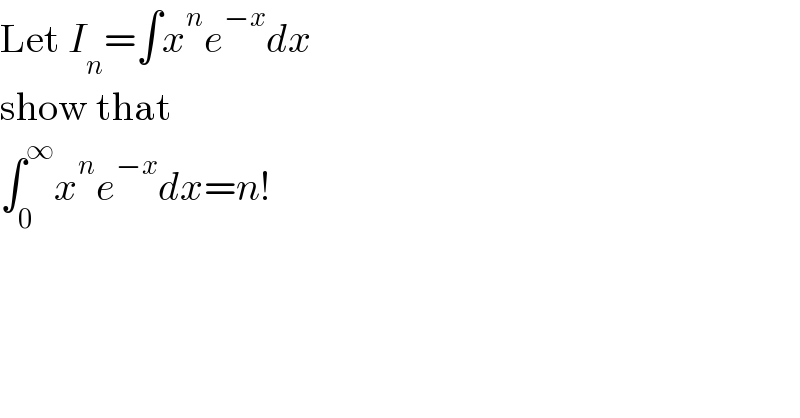
$$\mathrm{Let}\:{I}_{{n}} =\int{x}^{{n}} {e}^{−{x}} {dx} \\ $$$$\mathrm{show}\:\mathrm{that}\: \\ $$$$\int_{\mathrm{0}} ^{\infty} {x}^{{n}} {e}^{−{x}} {dx}={n}! \\ $$
Answered by ArielVyny last updated on 23/Sep/21

$${use}\:{gamma}\:{function}. \\ $$$$\Gamma\left({m}\right)=\int_{\mathrm{0}} ^{\infty} {e}^{−{x}} {x}^{{m}−\mathrm{1}} {dx}\:{and}\:{we}\:{know}\:{that} \\ $$$$\Gamma\left({m}+\mathrm{1}\right)={m}! \\ $$$${then}\:\int_{\mathrm{0}} ^{\infty} {x}^{{n}} {e}^{−{x}} {dx}=\Gamma\left({n}+\mathrm{1}\right)={n}! \\ $$
