Question Number 156575 by MathSh last updated on 12/Oct/21
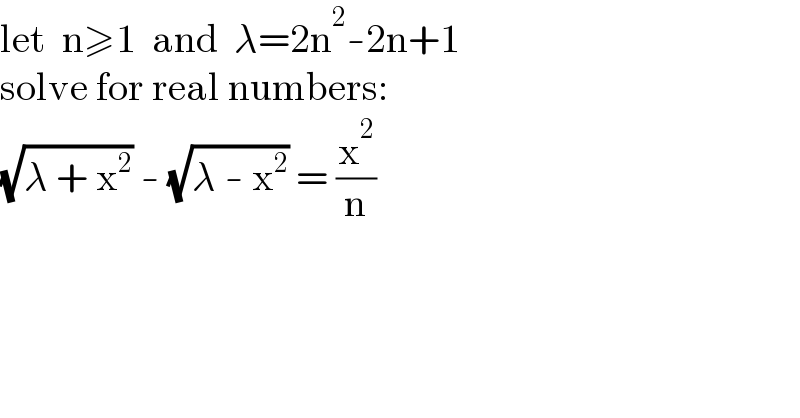
$$\mathrm{let}\:\:\mathrm{n}\geqslant\mathrm{1}\:\:\mathrm{and}\:\:\lambda=\mathrm{2n}^{\mathrm{2}} -\mathrm{2n}+\mathrm{1} \\ $$$$\mathrm{solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\sqrt{\lambda\:+\:\mathrm{x}^{\mathrm{2}} }\:-\:\sqrt{\lambda\:-\:\mathrm{x}^{\mathrm{2}} }\:=\:\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{n}} \\ $$
Commented by MathSh last updated on 13/Oct/21
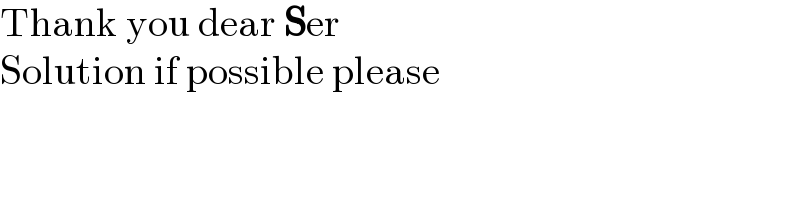
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$$$\mathrm{Solution}\:\mathrm{if}\:\mathrm{possible}\:\mathrm{please} \\ $$
Answered by mr W last updated on 13/Oct/21
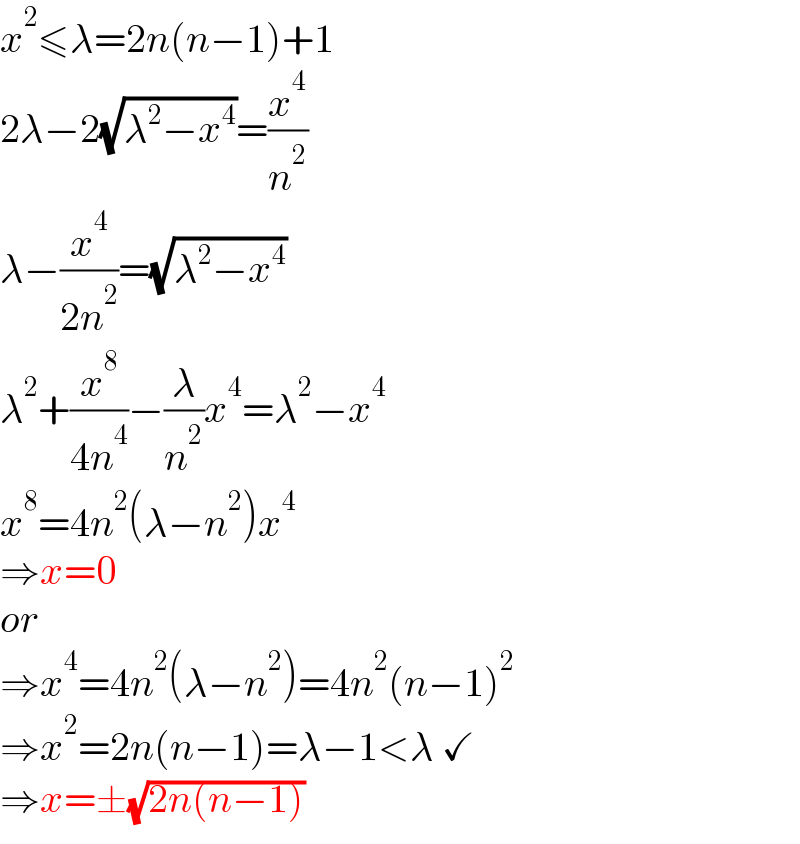
$${x}^{\mathrm{2}} \leqslant\lambda=\mathrm{2}{n}\left({n}−\mathrm{1}\right)+\mathrm{1} \\ $$$$\mathrm{2}\lambda−\mathrm{2}\sqrt{\lambda^{\mathrm{2}} −{x}^{\mathrm{4}} }=\frac{{x}^{\mathrm{4}} }{{n}^{\mathrm{2}} } \\ $$$$\lambda−\frac{{x}^{\mathrm{4}} }{\mathrm{2}{n}^{\mathrm{2}} }=\sqrt{\lambda^{\mathrm{2}} −{x}^{\mathrm{4}} } \\ $$$$\lambda^{\mathrm{2}} +\frac{{x}^{\mathrm{8}} }{\mathrm{4}{n}^{\mathrm{4}} }−\frac{\lambda}{{n}^{\mathrm{2}} }{x}^{\mathrm{4}} =\lambda^{\mathrm{2}} −{x}^{\mathrm{4}} \\ $$$${x}^{\mathrm{8}} =\mathrm{4}{n}^{\mathrm{2}} \left(\lambda−{n}^{\mathrm{2}} \right){x}^{\mathrm{4}} \\ $$$$\Rightarrow{x}=\mathrm{0} \\ $$$${or} \\ $$$$\Rightarrow{x}^{\mathrm{4}} =\mathrm{4}{n}^{\mathrm{2}} \left(\lambda−{n}^{\mathrm{2}} \right)=\mathrm{4}{n}^{\mathrm{2}} \left({n}−\mathrm{1}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} =\mathrm{2}{n}\left({n}−\mathrm{1}\right)=\lambda−\mathrm{1}<\lambda\:\checkmark \\ $$$$\Rightarrow{x}=\pm\sqrt{\mathrm{2}{n}\left({n}−\mathrm{1}\right)} \\ $$
Commented by MathSh last updated on 13/Oct/21
$$\mathrm{Perfect}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{thankyou} \\ $$
