Question Number 21933 by Tinkutara last updated on 07/Oct/17
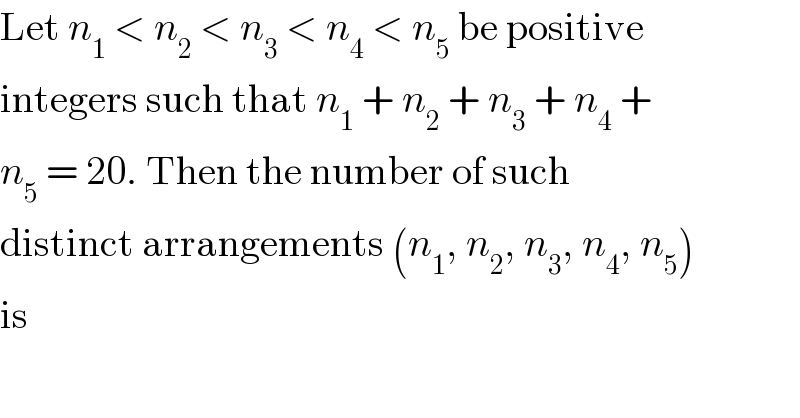
$$\mathrm{Let}\:{n}_{\mathrm{1}} \:<\:{n}_{\mathrm{2}} \:<\:{n}_{\mathrm{3}} \:<\:{n}_{\mathrm{4}} \:<\:{n}_{\mathrm{5}} \:\mathrm{be}\:\mathrm{positive} \\ $$$$\mathrm{integers}\:\mathrm{such}\:\mathrm{that}\:{n}_{\mathrm{1}} \:+\:{n}_{\mathrm{2}} \:+\:{n}_{\mathrm{3}} \:+\:{n}_{\mathrm{4}} \:+ \\ $$$${n}_{\mathrm{5}} \:=\:\mathrm{20}.\:\mathrm{Then}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{such} \\ $$$$\mathrm{distinct}\:\mathrm{arrangements}\:\left({n}_{\mathrm{1}} ,\:{n}_{\mathrm{2}} ,\:{n}_{\mathrm{3}} ,\:{n}_{\mathrm{4}} ,\:{n}_{\mathrm{5}} \right) \\ $$$$\mathrm{is} \\ $$
Commented by mrW1 last updated on 08/Oct/17
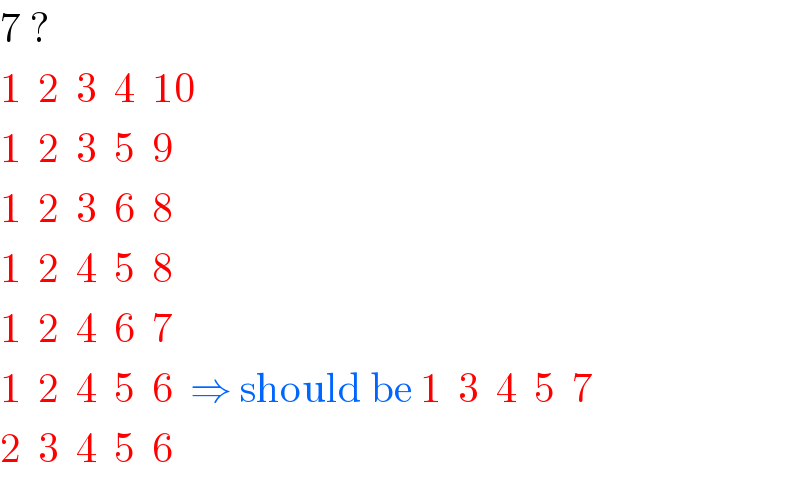
$$\mathrm{7}\:? \\ $$$$\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{3}\:\:\mathrm{4}\:\:\mathrm{10} \\ $$$$\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{3}\:\:\mathrm{5}\:\:\mathrm{9} \\ $$$$\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{3}\:\:\mathrm{6}\:\:\mathrm{8} \\ $$$$\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{4}\:\:\mathrm{5}\:\:\mathrm{8} \\ $$$$\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{4}\:\:\mathrm{6}\:\:\mathrm{7} \\ $$$$\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{4}\:\:\mathrm{5}\:\:\mathrm{6}\:\:\Rightarrow\:\mathrm{should}\:\mathrm{be}\:\mathrm{1}\:\:\mathrm{3}\:\:\mathrm{4}\:\:\mathrm{5}\:\:\mathrm{7} \\ $$$$\mathrm{2}\:\:\mathrm{3}\:\:\mathrm{4}\:\:\mathrm{5}\:\:\mathrm{6} \\ $$
Commented by Rasheed.Sindhi last updated on 08/Oct/17

$$\mathrm{1}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{7} \\ $$
Commented by Rasheed.Sindhi last updated on 08/Oct/17
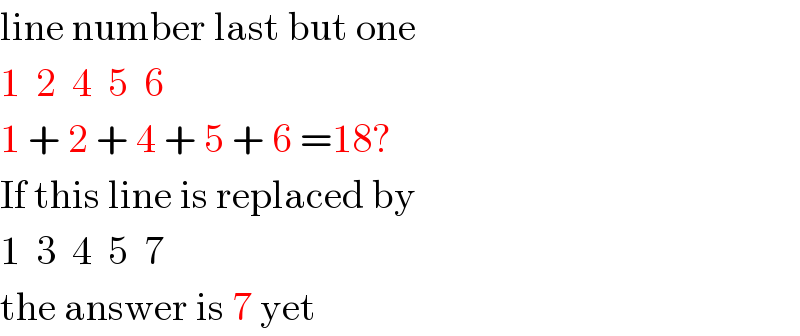
$$\mathrm{line}\:\mathrm{number}\:\mathrm{last}\:\mathrm{but}\:\mathrm{one} \\ $$$$\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{4}\:\:\mathrm{5}\:\:\mathrm{6} \\ $$$$\mathrm{1}\:+\:\mathrm{2}\:+\:\mathrm{4}\:+\:\mathrm{5}\:+\:\mathrm{6}\:=\mathrm{18}? \\ $$$$\mathrm{If}\:\mathrm{this}\:\mathrm{line}\:\mathrm{is}\:\mathrm{replaced}\:\mathrm{by} \\ $$$$\mathrm{1}\:\:\mathrm{3}\:\:\mathrm{4}\:\:\mathrm{5}\:\:\mathrm{7} \\ $$$$\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{7}\:\mathrm{yet} \\ $$
Commented by Tinkutara last updated on 08/Oct/17

$$\mathrm{mrW1},\:\mathrm{why}\:\mathrm{you}\:\mathrm{don}'\mathrm{t}\:\mathrm{take}\:\mathrm{1}+\mathrm{3}+\mathrm{4}+\mathrm{5}+\mathrm{7}? \\ $$$$\mathrm{But}\:\mathrm{your}\:\mathrm{answer}\:\mathrm{7}\:\mathrm{is}\:\mathrm{correct}. \\ $$
Commented by mrW1 last updated on 08/Oct/17
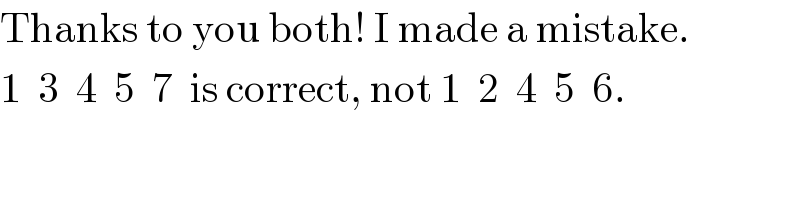
$$\mathrm{Thanks}\:\mathrm{to}\:\mathrm{you}\:\mathrm{both}!\:\mathrm{I}\:\mathrm{made}\:\mathrm{a}\:\mathrm{mistake}. \\ $$$$\mathrm{1}\:\:\mathrm{3}\:\:\mathrm{4}\:\:\mathrm{5}\:\:\mathrm{7}\:\:\mathrm{is}\:\mathrm{correct},\:\mathrm{not}\:\mathrm{1}\:\:\mathrm{2}\:\:\mathrm{4}\:\:\mathrm{5}\:\:\mathrm{6}. \\ $$
Commented by mrW1 last updated on 09/Oct/17
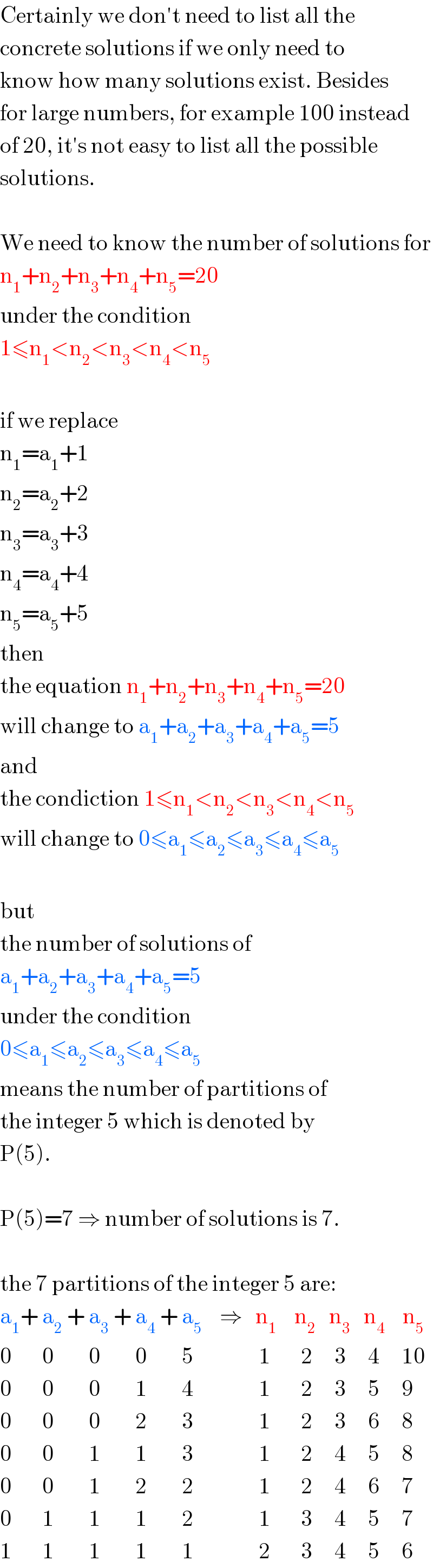
$$\mathrm{Certainly}\:\mathrm{we}\:\mathrm{don}'\mathrm{t}\:\mathrm{need}\:\mathrm{to}\:\mathrm{list}\:\mathrm{all}\:\mathrm{the} \\ $$$$\mathrm{concrete}\:\mathrm{solutions}\:\mathrm{if}\:\mathrm{we}\:\mathrm{only}\:\mathrm{need}\:\mathrm{to} \\ $$$$\mathrm{know}\:\mathrm{how}\:\mathrm{many}\:\mathrm{solutions}\:\mathrm{exist}.\:\mathrm{Besides} \\ $$$$\mathrm{for}\:\mathrm{large}\:\mathrm{numbers},\:\mathrm{for}\:\mathrm{example}\:\mathrm{100}\:\mathrm{instead} \\ $$$$\mathrm{of}\:\mathrm{20},\:\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{easy}\:\mathrm{to}\:\mathrm{list}\:\mathrm{all}\:\mathrm{the}\:\mathrm{possible} \\ $$$$\mathrm{solutions}. \\ $$$$ \\ $$$$\mathrm{We}\:\mathrm{need}\:\mathrm{to}\:\mathrm{know}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{for} \\ $$$$\mathrm{n}_{\mathrm{1}} +\mathrm{n}_{\mathrm{2}} +\mathrm{n}_{\mathrm{3}} +\mathrm{n}_{\mathrm{4}} +\mathrm{n}_{\mathrm{5}} =\mathrm{20} \\ $$$$\mathrm{under}\:\mathrm{the}\:\mathrm{condition} \\ $$$$\mathrm{1}\leqslant\mathrm{n}_{\mathrm{1}} <\mathrm{n}_{\mathrm{2}} <\mathrm{n}_{\mathrm{3}} <\mathrm{n}_{\mathrm{4}} <\mathrm{n}_{\mathrm{5}} \\ $$$$ \\ $$$$\mathrm{if}\:\mathrm{we}\:\mathrm{replace} \\ $$$$\mathrm{n}_{\mathrm{1}} =\mathrm{a}_{\mathrm{1}} +\mathrm{1} \\ $$$$\mathrm{n}_{\mathrm{2}} =\mathrm{a}_{\mathrm{2}} +\mathrm{2} \\ $$$$\mathrm{n}_{\mathrm{3}} =\mathrm{a}_{\mathrm{3}} +\mathrm{3} \\ $$$$\mathrm{n}_{\mathrm{4}} =\mathrm{a}_{\mathrm{4}} +\mathrm{4} \\ $$$$\mathrm{n}_{\mathrm{5}} =\mathrm{a}_{\mathrm{5}} +\mathrm{5} \\ $$$$\mathrm{then} \\ $$$$\mathrm{the}\:\mathrm{equation}\:\mathrm{n}_{\mathrm{1}} +\mathrm{n}_{\mathrm{2}} +\mathrm{n}_{\mathrm{3}} +\mathrm{n}_{\mathrm{4}} +\mathrm{n}_{\mathrm{5}} =\mathrm{20} \\ $$$$\mathrm{will}\:\mathrm{change}\:\mathrm{to}\:\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} +\mathrm{a}_{\mathrm{3}} +\mathrm{a}_{\mathrm{4}} +\mathrm{a}_{\mathrm{5}} =\mathrm{5} \\ $$$$\mathrm{and} \\ $$$$\mathrm{the}\:\mathrm{condiction}\:\mathrm{1}\leqslant\mathrm{n}_{\mathrm{1}} <\mathrm{n}_{\mathrm{2}} <\mathrm{n}_{\mathrm{3}} <\mathrm{n}_{\mathrm{4}} <\mathrm{n}_{\mathrm{5}} \\ $$$$\mathrm{will}\:\mathrm{change}\:\mathrm{to}\:\mathrm{0}\leqslant\mathrm{a}_{\mathrm{1}} \leqslant\mathrm{a}_{\mathrm{2}} \leqslant\mathrm{a}_{\mathrm{3}} \leqslant\mathrm{a}_{\mathrm{4}} \leqslant\mathrm{a}_{\mathrm{5}} \\ $$$$ \\ $$$$\mathrm{but} \\ $$$$\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{of} \\ $$$$\mathrm{a}_{\mathrm{1}} +\mathrm{a}_{\mathrm{2}} +\mathrm{a}_{\mathrm{3}} +\mathrm{a}_{\mathrm{4}} +\mathrm{a}_{\mathrm{5}} =\mathrm{5} \\ $$$$\mathrm{under}\:\mathrm{the}\:\mathrm{condition} \\ $$$$\mathrm{0}\leqslant\mathrm{a}_{\mathrm{1}} \leqslant\mathrm{a}_{\mathrm{2}} \leqslant\mathrm{a}_{\mathrm{3}} \leqslant\mathrm{a}_{\mathrm{4}} \leqslant\mathrm{a}_{\mathrm{5}} \\ $$$$\mathrm{means}\:\mathrm{the}\:\mathrm{number}\:\mathrm{of}\:\mathrm{partitions}\:\mathrm{of} \\ $$$$\mathrm{the}\:\mathrm{integer}\:\mathrm{5}\:\mathrm{which}\:\mathrm{is}\:\mathrm{denoted}\:\mathrm{by} \\ $$$$\mathrm{P}\left(\mathrm{5}\right). \\ $$$$ \\ $$$$\mathrm{P}\left(\mathrm{5}\right)=\mathrm{7}\:\Rightarrow\:\mathrm{number}\:\mathrm{of}\:\mathrm{solutions}\:\mathrm{is}\:\mathrm{7}. \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{7}\:\mathrm{partitions}\:\mathrm{of}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{5}\:\mathrm{are}: \\ $$$$\mathrm{a}_{\mathrm{1}} +\:\mathrm{a}_{\mathrm{2}} \:+\:\mathrm{a}_{\mathrm{3}} \:+\:\mathrm{a}_{\mathrm{4}} \:+\:\mathrm{a}_{\mathrm{5}} \:\:\:\:\Rightarrow\:\:\:\mathrm{n}_{\mathrm{1}} \:\:\:\:\mathrm{n}_{\mathrm{2}} \:\:\:\mathrm{n}_{\mathrm{3}} \:\:\:\mathrm{n}_{\mathrm{4}} \:\:\:\:\mathrm{n}_{\mathrm{5}} \\ $$$$\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{5}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{4}\:\:\:\:\:\mathrm{10} \\ $$$$\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{4}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{5}\:\:\:\:\:\mathrm{9} \\ $$$$\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{6}\:\:\:\:\:\mathrm{8} \\ $$$$\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{4}\:\:\:\:\:\mathrm{5}\:\:\:\:\:\mathrm{8} \\ $$$$\mathrm{0}\:\:\:\:\:\:\:\mathrm{0}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\mathrm{4}\:\:\:\:\:\mathrm{6}\:\:\:\:\:\mathrm{7} \\ $$$$\mathrm{0}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{4}\:\:\:\:\:\mathrm{5}\:\:\:\:\:\mathrm{7} \\ $$$$\mathrm{1}\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{2}\:\:\:\:\:\:\:\mathrm{3}\:\:\:\:\:\mathrm{4}\:\:\:\:\:\mathrm{5}\:\:\:\:\:\mathrm{6} \\ $$
Commented by Tinkutara last updated on 08/Oct/17
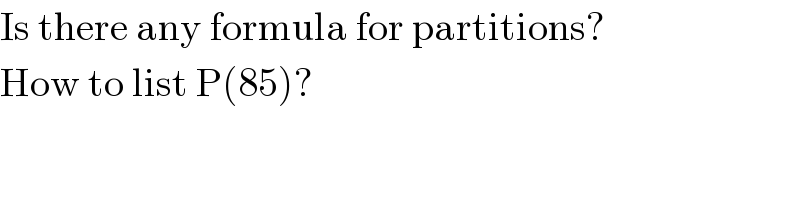
$$\mathrm{Is}\:\mathrm{there}\:\mathrm{any}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{partitions}? \\ $$$$\mathrm{How}\:\mathrm{to}\:\mathrm{list}\:\mathrm{P}\left(\mathrm{85}\right)? \\ $$
Commented by mrW1 last updated on 09/Oct/17

$$\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{formula}\:\mathrm{to}\:\mathrm{calculate}\:\mathrm{the} \\ $$$$\mathrm{integer}\:\mathrm{partitions}\:\mathrm{directly}.\:\mathrm{usually}\:\mathrm{we} \\ $$$$\mathrm{use}\:\mathrm{generating}\:\mathrm{functions}. \\ $$
Commented by Tinkutara last updated on 09/Oct/17

$$\mathrm{Got}\:\mathrm{it}. \\ $$
Commented by mrW1 last updated on 09/Oct/17

$$\mathrm{mr}.\:\mathrm{ajfour}\:\mathrm{had}\:\mathrm{an}\:\mathrm{example}\:\mathrm{in}\:\mathrm{Q21802} \\ $$$$\mathrm{for}\:\mathrm{using}\:\mathrm{generating}\:\mathrm{function}\:\mathrm{to}\:\mathrm{find} \\ $$$$\mathrm{number}\:\mathrm{of}\:\mathrm{integer}\:\mathrm{solutions}.\:\mathrm{it}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{really}\:\mathrm{a}\:\mathrm{function}\:\mathrm{but}\:\mathrm{a}\:\mathrm{method}. \\ $$
Commented by mrW1 last updated on 09/Oct/17

$$\mathrm{see}\:\mathrm{also}\:\mathrm{Q21800} \\ $$
