Question Number 120188 by benjo_mathlover last updated on 30/Oct/20
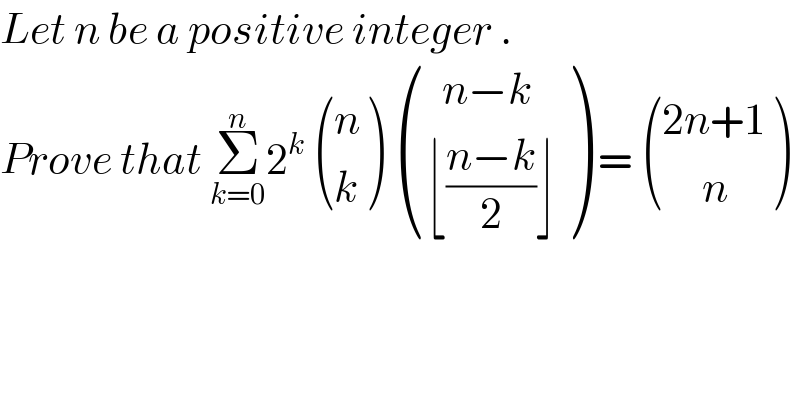
$${Let}\:{n}\:{be}\:{a}\:{positive}\:{integer}\:. \\ $$$${Prove}\:{that}\:\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \:\begin{pmatrix}{{n}}\\{{k}}\end{pmatrix}\:\begin{pmatrix}{\:\:{n}−{k}}\\{\lfloor\frac{{n}−{k}}{\mathrm{2}}\rfloor}\end{pmatrix}\:=\:\begin{pmatrix}{\mathrm{2}{n}+\mathrm{1}}\\{\:\:\:\:\:{n}}\end{pmatrix} \\ $$
