Let-n-be-the-sum-of-all-positive-divisors-of-the-integer-n-and-let-p-be-any-prime-number-show-that-n-lt-2n-holds-true-for-all-n-of-the-form-n-p-2-Mastermind-

Question Number 174594 by Mastermind last updated on 05/Aug/22

$$\mathrm{Let}\:\sigma\left(\mathrm{n}\right)\:\mathrm{be}\:\mathrm{the}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{all}\:\mathrm{positive} \\ $$$$\mathrm{divisors}\:\mathrm{of}\:\mathrm{the}\:\mathrm{integer}\:\mathrm{n}\:\mathrm{and}\:\mathrm{let}\:\mathrm{p}\:\mathrm{be} \\ $$$$\mathrm{any}\:\mathrm{prime}\:\mathrm{number}.\:\mathrm{show}\:\mathrm{that}\: \\ $$$$\sigma\left(\mathrm{n}\right)<\mathrm{2n}\:\mathrm{holds}\:\mathrm{true}\:\mathrm{for}\:\mathrm{all}\:\mathrm{n}\:\mathrm{of}\:\mathrm{the}\: \\ $$$$\mathrm{form}\:\mathrm{n}=\mathrm{p}^{\mathrm{2}} . \\ $$$$ \\ $$$$\mathrm{Mastermind} \\ $$

Answered by floor(10²Eta[1]) last updated on 05/Aug/22

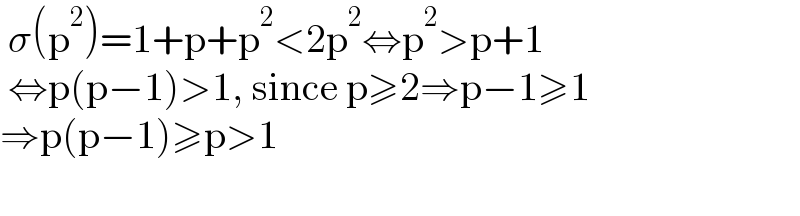
$$\:\sigma\left(\mathrm{p}^{\mathrm{2}} \right)=\mathrm{1}+\mathrm{p}+\mathrm{p}^{\mathrm{2}} <\mathrm{2p}^{\mathrm{2}} \Leftrightarrow\mathrm{p}^{\mathrm{2}} >\mathrm{p}+\mathrm{1} \\ $$$$\:\Leftrightarrow\mathrm{p}\left(\mathrm{p}−\mathrm{1}\right)>\mathrm{1},\:\mathrm{since}\:\mathrm{p}\geqslant\mathrm{2}\Rightarrow\mathrm{p}−\mathrm{1}\geqslant\mathrm{1} \\ $$$$\Rightarrow\mathrm{p}\left(\mathrm{p}−\mathrm{1}\right)\geqslant\mathrm{p}>\mathrm{1} \\ $$$$ \\ $$

Commented by Mastermind last updated on 05/Aug/22

$$\mathrm{Thanks} \\ $$

Commented by Mastermind last updated on 06/Aug/22

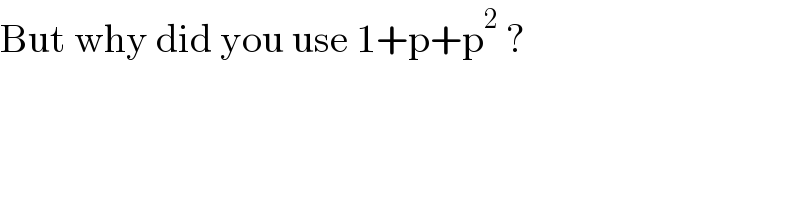
$$\mathrm{But}\:\mathrm{why}\:\mathrm{did}\:\mathrm{you}\:\mathrm{use}\:\mathrm{1}+\mathrm{p}+\mathrm{p}^{\mathrm{2}} \:? \\ $$

Terms of Service
Privacy Policy
Contact: info@tinkutara.com