Question Number 173150 by Frix last updated on 07/Jul/22
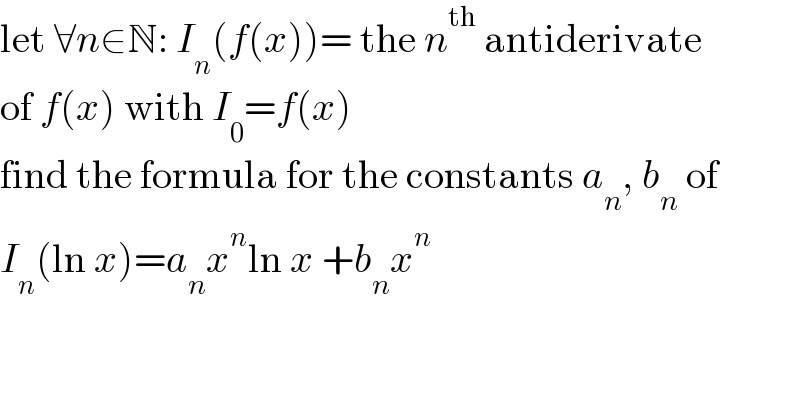
$$\mathrm{let}\:\forall{n}\in\mathbb{N}:\:{I}_{{n}} \left({f}\left({x}\right)\right)=\:\mathrm{the}\:{n}^{\mathrm{th}} \:\mathrm{antiderivate} \\ $$$$\mathrm{of}\:{f}\left({x}\right)\:\mathrm{with}\:{I}_{\mathrm{0}} ={f}\left({x}\right) \\ $$$$\mathrm{find}\:\mathrm{the}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{the}\:\mathrm{constants}\:{a}_{{n}} ,\:{b}_{{n}} \:\mathrm{of} \\ $$$${I}_{{n}} \left(\mathrm{ln}\:{x}\right)={a}_{{n}} {x}^{{n}} \mathrm{ln}\:{x}\:+{b}_{{n}} {x}^{{n}} \\ $$
Answered by aleks041103 last updated on 07/Jul/22
![I_(n+1) (ln x)=∫I_n (ln x)dx= =∫(a_n x^n ln x + b_n x^n )dx= =a_n ∫x^n ln x dx + b_n ∫x^n dx ∫x^n ln x dx=∫ln x d((x^(n+1) /(n+1)))= =(x^(n+1) /(n+1))ln x−(1/(n+1))∫x^(n+1) (dx/x)= =(1/(n+1))x^(n+1) ln x −(1/((n+1)^2 ))x^(n+1) ⇒I_(n+1) (ln x)=a_n [(1/(n+1))x^(n+1) ln x −(1/((n+1)^2 ))x^(n+1) ]+(b_n /(n+1))x^(n+1) = =((a_n /(n+1)))x^(n+1) ln x + ((b_n /(n+1))−(a_n /((n+1)^2 )))x^(n+1) = =a_(n+1) x^(n+1) ln x + b_(n+1) x^(n+1) ⇒ { ((a_(n+1) =(a_n /(n+1)))),((b_(n+1) =(b_n /(n+1))−(a_n /((n+1)^2 )))) :} (1/a_(n+1) )=(n+1)(1/a_n )⇒(1/a_n )=const.n!⇒a_n =((const)/(n!)) I_0 (ln x)=ln x⇒a_0 =1⇒a_n =(1/(n!)) ⇒b_(n+1) =(b_n /(n+1))−(1/((n+1)!(n+1))) (n+1)b_(n+1) −b_n =−(1/((n+1)!)) b_n =(c_n /(n!)) ⇒(n+1)(c_(n+1) /((n+1)!))−(c_n /(n!))=−(1/((n+1)!))=−(1/((n+1) n!)) ⇒c_(n+1) −c_n =−(1/(n+1)) ⇒c_n =const.−Σ_(i≥1) ^n (1/i) c_0 =const.=0⇒c_n =−Σ_(i≥1) ^n (1/i)=−H_n ⇒b_n =−(H_n /(n!)) ⇒ { ((a_n =(1/(n!)))),((b_n =−(H_n /(n!)) , H_(n≥1) =Σ_(k=1) ^n (1/k), H_0 =0)) :}](https://www.tinkutara.com/question/Q173158.png)
$${I}_{{n}+\mathrm{1}} \left({ln}\:{x}\right)=\int{I}_{{n}} \left({ln}\:{x}\right){dx}= \\ $$$$=\int\left({a}_{{n}} {x}^{{n}} {ln}\:{x}\:+\:{b}_{{n}} {x}^{{n}} \right){dx}= \\ $$$$={a}_{{n}} \int{x}^{{n}} {ln}\:{x}\:{dx}\:+\:{b}_{{n}} \int{x}^{{n}} {dx} \\ $$$$\int{x}^{{n}} {ln}\:{x}\:{dx}=\int{ln}\:{x}\:{d}\left(\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}\right)= \\ $$$$=\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}{ln}\:{x}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\int{x}^{{n}+\mathrm{1}} \frac{{dx}}{{x}}= \\ $$$$=\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} {ln}\:{x}\:−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{x}^{{n}+\mathrm{1}} \\ $$$$\Rightarrow{I}_{{n}+\mathrm{1}} \left({ln}\:{x}\right)={a}_{{n}} \left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} {ln}\:{x}\:−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{x}^{{n}+\mathrm{1}} \right]+\frac{{b}_{{n}} }{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} = \\ $$$$=\left(\frac{{a}_{{n}} }{{n}+\mathrm{1}}\right){x}^{{n}+\mathrm{1}} {ln}\:{x}\:+\:\left(\frac{{b}_{{n}} }{{n}+\mathrm{1}}−\frac{{a}_{{n}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right){x}^{{n}+\mathrm{1}} = \\ $$$$={a}_{{n}+\mathrm{1}} {x}^{{n}+\mathrm{1}} {ln}\:{x}\:+\:{b}_{{n}+\mathrm{1}} {x}^{{n}+\mathrm{1}} \\ $$$$\Rightarrow\begin{cases}{{a}_{{n}+\mathrm{1}} =\frac{{a}_{{n}} }{{n}+\mathrm{1}}}\\{{b}_{{n}+\mathrm{1}} =\frac{{b}_{{n}} }{{n}+\mathrm{1}}−\frac{{a}_{{n}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }}\end{cases} \\ $$$$\frac{\mathrm{1}}{{a}_{{n}+\mathrm{1}} }=\left({n}+\mathrm{1}\right)\frac{\mathrm{1}}{{a}_{{n}} }\Rightarrow\frac{\mathrm{1}}{{a}_{{n}} }={const}.{n}!\Rightarrow{a}_{{n}} =\frac{{const}}{{n}!} \\ $$$${I}_{\mathrm{0}} \left({ln}\:{x}\right)={ln}\:{x}\Rightarrow{a}_{\mathrm{0}} =\mathrm{1}\Rightarrow{a}_{{n}} =\frac{\mathrm{1}}{{n}!} \\ $$$$\Rightarrow{b}_{{n}+\mathrm{1}} =\frac{{b}_{{n}} }{{n}+\mathrm{1}}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!\left({n}+\mathrm{1}\right)} \\ $$$$\left({n}+\mathrm{1}\right){b}_{{n}+\mathrm{1}} −{b}_{{n}} =−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$${b}_{{n}} =\frac{{c}_{{n}} }{{n}!} \\ $$$$\Rightarrow\left({n}+\mathrm{1}\right)\frac{{c}_{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)!}−\frac{{c}_{{n}} }{{n}!}=−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!}=−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)\:{n}!} \\ $$$$\Rightarrow{c}_{{n}+\mathrm{1}} −{c}_{{n}} =−\frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\Rightarrow{c}_{{n}} ={const}.−\underset{{i}\geqslant\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{i}} \\ $$$${c}_{\mathrm{0}} ={const}.=\mathrm{0}\Rightarrow{c}_{{n}} =−\underset{{i}\geqslant\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{i}}=−{H}_{{n}} \\ $$$$\Rightarrow{b}_{{n}} =−\frac{{H}_{{n}} }{{n}!} \\ $$$$\Rightarrow\begin{cases}{{a}_{{n}} =\frac{\mathrm{1}}{{n}!}}\\{{b}_{{n}} =−\frac{{H}_{{n}} }{{n}!}\:,\:{H}_{{n}\geqslant\mathrm{1}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{{k}},\:{H}_{\mathrm{0}} =\mathrm{0}}\end{cases} \\ $$
Commented by Frix last updated on 08/Jul/22

$$\mathrm{thank}\:\mathrm{you}! \\ $$
Commented by Tawa11 last updated on 11/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
