Question Number 155154 by mathdanisur last updated on 26/Sep/21
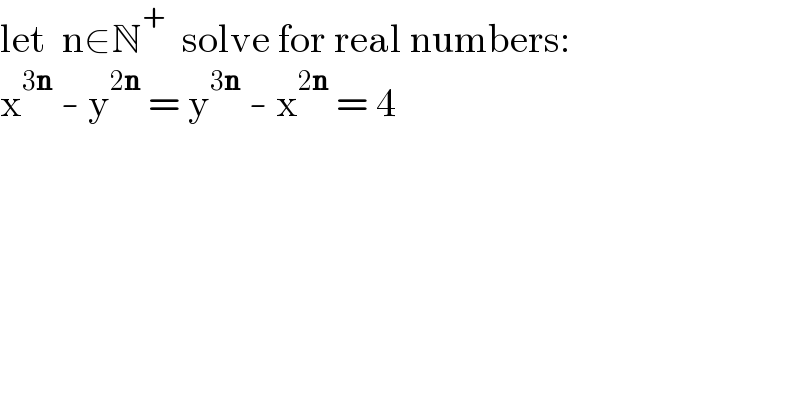
$$\mathrm{let}\:\:\mathrm{n}\in\mathbb{N}^{+} \:\:\mathrm{solve}\:\mathrm{for}\:\mathrm{real}\:\mathrm{numbers}: \\ $$$$\mathrm{x}^{\mathrm{3}\boldsymbol{\mathrm{n}}} \:-\:\mathrm{y}^{\mathrm{2}\boldsymbol{\mathrm{n}}} \:=\:\mathrm{y}^{\mathrm{3}\boldsymbol{\mathrm{n}}} \:-\:\mathrm{x}^{\mathrm{2}\boldsymbol{\mathrm{n}}} \:=\:\mathrm{4} \\ $$
Answered by MJS_new last updated on 26/Sep/21
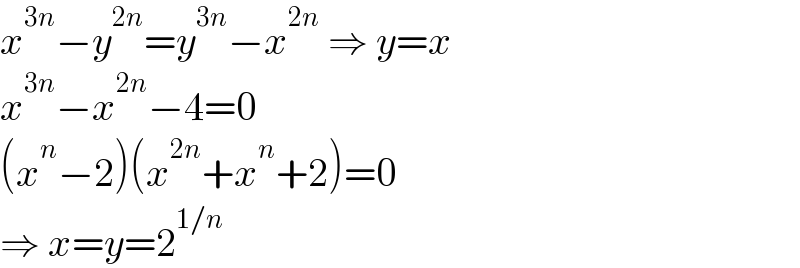
$${x}^{\mathrm{3}{n}} −{y}^{\mathrm{2}{n}} ={y}^{\mathrm{3}{n}} −{x}^{\mathrm{2}{n}} \:\Rightarrow\:{y}={x} \\ $$$${x}^{\mathrm{3}{n}} −{x}^{\mathrm{2}{n}} −\mathrm{4}=\mathrm{0} \\ $$$$\left({x}^{{n}} −\mathrm{2}\right)\left({x}^{\mathrm{2}{n}} +{x}^{{n}} +\mathrm{2}\right)=\mathrm{0} \\ $$$$\Rightarrow\:{x}={y}=\mathrm{2}^{\mathrm{1}/{n}} \\ $$
Commented by mathdanisur last updated on 26/Sep/21
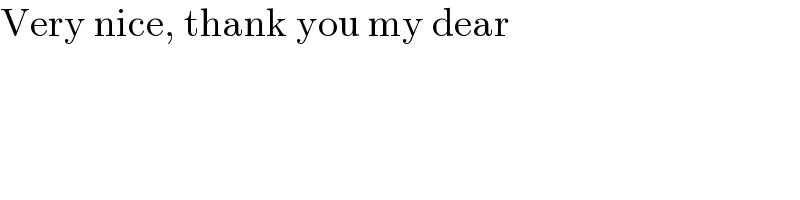
$$\mathrm{Very}\:\mathrm{nice},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{my}\:\mathrm{dear} \\ $$
