Menu Close

Let-n-Z-f-1-1-f-2n-f-n-f-2n-1-f-n-2-2-f-1-f-2-f-3-f-100-

Tinku Tara 0 Comments
Pin




Question Number 47477 by naka3546 last updated on 10/Nov/18
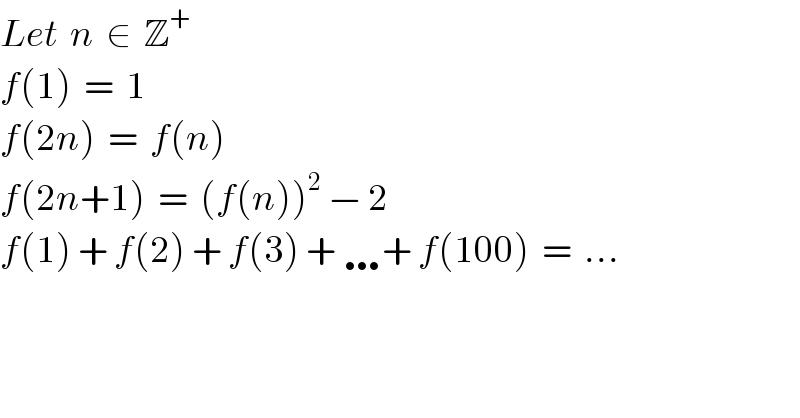
Let n ∈ Z^+ f(1) = 1 f(2n) = f(n) f(2n+1) = (f(n))^2 − 2 f(1) + f(2) + f(3) + …+ f(100) = ...
$${Let}\:\:{n}\:\:\in\:\:\mathbb{Z}^{+} \\ $$$${f}\left(\mathrm{1}\right)\:\:=\:\:\mathrm{1} \\ $$$${f}\left(\mathrm{2}{n}\right)\:\:=\:\:{f}\left({n}\right) \\ $$$${f}\left(\mathrm{2}{n}+\mathrm{1}\right)\:\:=\:\:\left({f}\left({n}\right)\right)^{\mathrm{2}} \:−\:\mathrm{2} \\ $$$${f}\left(\mathrm{1}\right)\:+\:{f}\left(\mathrm{2}\right)\:+\:{f}\left(\mathrm{3}\right)\:+\:\ldots+\:{f}\left(\mathrm{100}\right)\:\:=\:\:… \\ $$
Answered by MJS last updated on 11/Nov/18
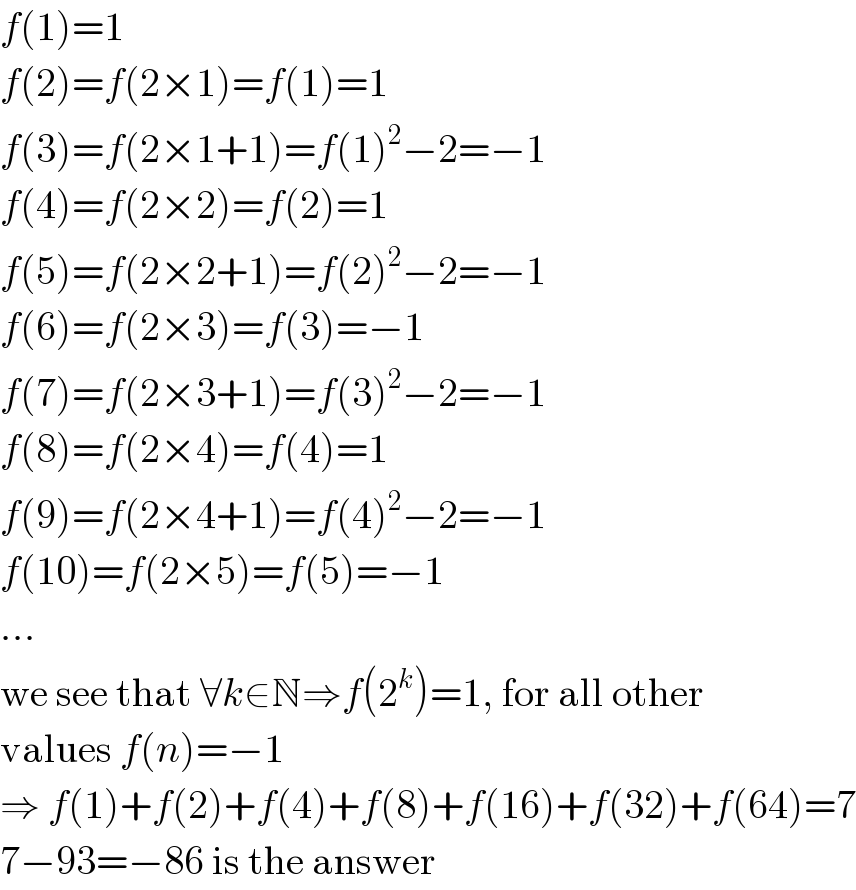
f(1)=1 f(2)=f(2×1)=f(1)=1 f(3)=f(2×1+1)=f(1)^2 −2=−1 f(4)=f(2×2)=f(2)=1 f(5)=f(2×2+1)=f(2)^2 −2=−1 f(6)=f(2×3)=f(3)=−1 f(7)=f(2×3+1)=f(3)^2 −2=−1 f(8)=f(2×4)=f(4)=1 f(9)=f(2×4+1)=f(4)^2 −2=−1 f(10)=f(2×5)=f(5)=−1 ... we see that ∀k∈N⇒f(2^k )=1, for all other values f(n)=−1 ⇒ f(1)+f(2)+f(4)+f(8)+f(16)+f(32)+f(64)=7 7−93=−86 is the answer
$${f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{2}\right)={f}\left(\mathrm{2}×\mathrm{1}\right)={f}\left(\mathrm{1}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{3}\right)={f}\left(\mathrm{2}×\mathrm{1}+\mathrm{1}\right)={f}\left(\mathrm{1}\right)^{\mathrm{2}} −\mathrm{2}=−\mathrm{1} \\ $$$${f}\left(\mathrm{4}\right)={f}\left(\mathrm{2}×\mathrm{2}\right)={f}\left(\mathrm{2}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{5}\right)={f}\left(\mathrm{2}×\mathrm{2}+\mathrm{1}\right)={f}\left(\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}=−\mathrm{1} \\ $$$${f}\left(\mathrm{6}\right)={f}\left(\mathrm{2}×\mathrm{3}\right)={f}\left(\mathrm{3}\right)=−\mathrm{1} \\ $$$${f}\left(\mathrm{7}\right)={f}\left(\mathrm{2}×\mathrm{3}+\mathrm{1}\right)={f}\left(\mathrm{3}\right)^{\mathrm{2}} −\mathrm{2}=−\mathrm{1} \\ $$$${f}\left(\mathrm{8}\right)={f}\left(\mathrm{2}×\mathrm{4}\right)={f}\left(\mathrm{4}\right)=\mathrm{1} \\ $$$${f}\left(\mathrm{9}\right)={f}\left(\mathrm{2}×\mathrm{4}+\mathrm{1}\right)={f}\left(\mathrm{4}\right)^{\mathrm{2}} −\mathrm{2}=−\mathrm{1} \\ $$$${f}\left(\mathrm{10}\right)={f}\left(\mathrm{2}×\mathrm{5}\right)={f}\left(\mathrm{5}\right)=−\mathrm{1} \\ $$$$… \\ $$$$\mathrm{we}\:\mathrm{see}\:\mathrm{that}\:\forall{k}\in\mathbb{N}\Rightarrow{f}\left(\mathrm{2}^{{k}} \right)=\mathrm{1},\:\mathrm{for}\:\mathrm{all}\:\mathrm{other} \\ $$$$\mathrm{values}\:{f}\left({n}\right)=−\mathrm{1} \\ $$$$\Rightarrow\:{f}\left(\mathrm{1}\right)+{f}\left(\mathrm{2}\right)+{f}\left(\mathrm{4}\right)+{f}\left(\mathrm{8}\right)+{f}\left(\mathrm{16}\right)+{f}\left(\mathrm{32}\right)+{f}\left(\mathrm{64}\right)=\mathrm{7} \\ $$$$\mathrm{7}−\mathrm{93}=−\mathrm{86}\:\mathrm{is}\:\mathrm{the}\:\mathrm{answer} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *