Question Number 42196 by rahul 19 last updated on 20/Aug/18

$$\mathrm{Let}\:\mathrm{P}\:\mathrm{be}\:\mathrm{an}\:\mathrm{interior}\:\mathrm{point}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle} \\ $$$$\mathrm{ABC}\:\mathrm{and}\:\mathrm{AP},\mathrm{BP},\mathrm{CP}\:\mathrm{meet}\:\mathrm{the}\:\mathrm{sides}\:\mathrm{BC}, \\ $$$$\mathrm{CA},\mathrm{AB}\:\mathrm{in}\:\mathrm{D},\mathrm{E},\mathrm{F}\:\mathrm{respectively}.\:\mathrm{Show} \\ $$$$\mathrm{that}\:\frac{\mathrm{AP}}{\mathrm{PD}}=\:\frac{\mathrm{AF}}{\mathrm{FB}}\:+\:\frac{\mathrm{AE}}{\mathrm{EC}}\:. \\ $$
Commented by rahul 19 last updated on 20/Aug/18

$$\mathrm{Again}\:\mathrm{do}\:\mathrm{by}\:\mathrm{concept}\:\mathrm{of}\:\mathrm{vectors}\:\mathrm{only}! \\ $$
Commented by ajfour last updated on 20/Aug/18
Commented by ajfour last updated on 21/Aug/18
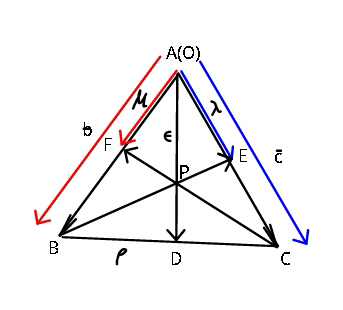
![to prove ((AF)/(FB)) +((AE)/(EC)) = ((AP)/(PD)) let AF = μb^� ; AE=λc^� AP = ε AD ⇒ To prove : (μ/(1−μ))+(λ/(1−λ))=(ε/(1−ε)) p^� = b^� +l(λc^� −b^� ) = c^� +m(μb^� −c^� ) = ε[b^� +ρ(c^� −b^� )] ⇒ 1−l = μm = ε−ερ ...(i) & λl = 1−m = ερ ....(ii) ⇒ 1−((ερ)/λ)=μ(1−ερ)=ε−ερ ⇒ ερ = ((1−μ)/((1/λ)−μ)) = ((1−ε)/((1/λ)−1)) ⇒ (1/λ)−1−(μ/λ)+μ = (1/λ)−μ−(ε/λ)+εμ ⇒ λ+μ−λμ = λμ+ε−λεμ ⇒ ε = ((λ+μ−2λμ)/(1−λμ)) (ε/(1−ε)) = ((λ+μ−2λμ)/(1−λ−μ+λμ)) =((μ(1−λ)+λ(1−μ))/((1−λ)(1−μ))) ⇒ (𝛆/(1−𝛆)) = (𝛍/(1−𝛍))+(𝛌/(1−𝛌)) .](https://www.tinkutara.com/question/Q42263.png)
$${to}\:{prove}\:\:\frac{{AF}}{{FB}}\:+\frac{{AE}}{{EC}}\:=\:\frac{{AP}}{{PD}} \\ $$$${let}\:\:{AF}\:=\:\mu\bar {{b}}\:\:;\:{AE}=\lambda\bar {{c}} \\ $$$$\:\:\:\:\:\:\:\:{AP}\:=\:\epsilon\:{AD} \\ $$$$\Rightarrow\:{To}\:{prove}\::\:\:\frac{\mu}{\mathrm{1}−\mu}+\frac{\lambda}{\mathrm{1}−\lambda}=\frac{\epsilon}{\mathrm{1}−\epsilon} \\ $$$$\bar {{p}}\:=\:\bar {{b}}+{l}\left(\lambda\bar {{c}}−\bar {{b}}\right) \\ $$$$\:\:\:\:=\:\:\bar {{c}}+{m}\left(\mu\bar {{b}}−\bar {{c}}\right) \\ $$$$\:\:\:=\:\epsilon\left[\bar {{b}}+\rho\left(\bar {{c}}−\bar {{b}}\right)\right] \\ $$$$\Rightarrow\:\:\mathrm{1}−{l}\:=\:\mu{m}\:=\:\epsilon−\epsilon\rho\:\:\:\:…\left({i}\right) \\ $$$$\&\:\:\:\:\:\lambda{l}\:=\:\mathrm{1}−{m}\:=\:\epsilon\rho\:\:\:\:\:\:\:….\left({ii}\right) \\ $$$$\Rightarrow\:\:\mathrm{1}−\frac{\epsilon\rho}{\lambda}=\mu\left(\mathrm{1}−\epsilon\rho\right)=\epsilon−\epsilon\rho \\ $$$$\Rightarrow\:\epsilon\rho\:=\:\frac{\mathrm{1}−\mu}{\frac{\mathrm{1}}{\lambda}−\mu}\:=\:\frac{\mathrm{1}−\epsilon}{\frac{\mathrm{1}}{\lambda}−\mathrm{1}} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{\lambda}−\mathrm{1}−\frac{\mu}{\lambda}+\mu\:=\:\frac{\mathrm{1}}{\lambda}−\mu−\frac{\epsilon}{\lambda}+\epsilon\mu \\ $$$$\Rightarrow\:\:\lambda+\mu−\lambda\mu\:=\:\lambda\mu+\epsilon−\lambda\epsilon\mu \\ $$$$\Rightarrow\:\:\epsilon\:=\:\frac{\lambda+\mu−\mathrm{2}\lambda\mu}{\mathrm{1}−\lambda\mu} \\ $$$$\:\:\:\:\:\:\:\:\frac{\epsilon}{\mathrm{1}−\epsilon}\:=\:\frac{\lambda+\mu−\mathrm{2}\lambda\mu}{\mathrm{1}−\lambda−\mu+\lambda\mu} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mu\left(\mathrm{1}−\lambda\right)+\lambda\left(\mathrm{1}−\mu\right)}{\left(\mathrm{1}−\lambda\right)\left(\mathrm{1}−\mu\right)} \\ $$$$\Rightarrow\:\:\frac{\boldsymbol{\epsilon}}{\mathrm{1}−\boldsymbol{\epsilon}}\:=\:\frac{\boldsymbol{\mu}}{\mathrm{1}−\boldsymbol{\mu}}+\frac{\boldsymbol{\lambda}}{\mathrm{1}−\boldsymbol{\lambda}}\:. \\ $$
Commented by rahul 19 last updated on 21/Aug/18
thank you sir!����
I will see later .
