Question Number 21228 by Tinkutara last updated on 16/Sep/17
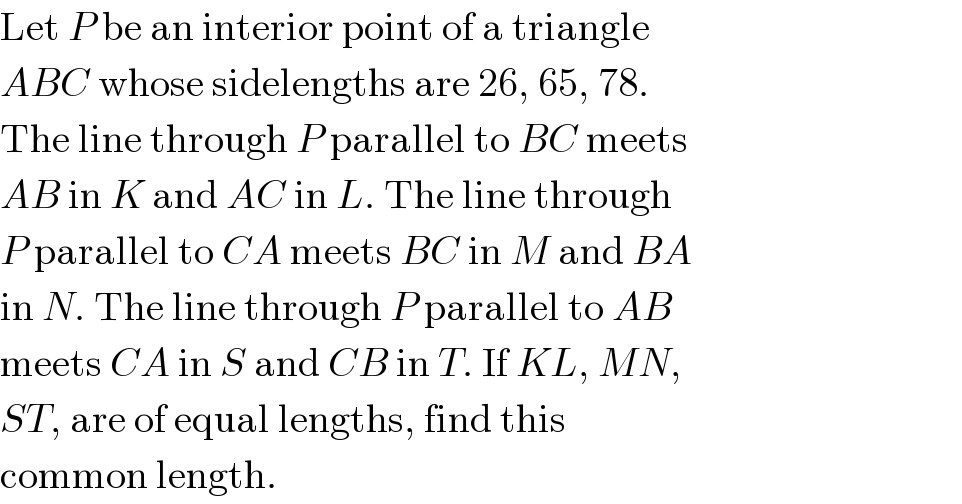
$$\mathrm{Let}\:{P}\:\mathrm{be}\:\mathrm{an}\:\mathrm{interior}\:\mathrm{point}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle} \\ $$$${ABC}\:\mathrm{whose}\:\mathrm{sidelengths}\:\mathrm{are}\:\mathrm{26},\:\mathrm{65},\:\mathrm{78}. \\ $$$$\mathrm{The}\:\mathrm{line}\:\mathrm{through}\:{P}\:\mathrm{parallel}\:\mathrm{to}\:{BC}\:\mathrm{meets} \\ $$$${AB}\:\mathrm{in}\:{K}\:\mathrm{and}\:{AC}\:\mathrm{in}\:{L}.\:\mathrm{The}\:\mathrm{line}\:\mathrm{through} \\ $$$${P}\:\mathrm{parallel}\:\mathrm{to}\:{CA}\:\mathrm{meets}\:{BC}\:\mathrm{in}\:{M}\:\mathrm{and}\:{BA} \\ $$$$\mathrm{in}\:{N}.\:\mathrm{The}\:\mathrm{line}\:\mathrm{through}\:{P}\:\mathrm{parallel}\:\mathrm{to}\:{AB} \\ $$$$\mathrm{meets}\:{CA}\:\mathrm{in}\:{S}\:\mathrm{and}\:{CB}\:\mathrm{in}\:{T}.\:\mathrm{If}\:{KL},\:{MN}, \\ $$$${ST},\:\mathrm{are}\:\mathrm{of}\:\mathrm{equal}\:\mathrm{lengths},\:\mathrm{find}\:\mathrm{this} \\ $$$$\mathrm{common}\:\mathrm{length}. \\ $$
