Menu Close

let-p-x-x-3-3x-4-find-and-

Tinku Tara 0 Comments
Pin




Question Number 39879 by Rio Mike last updated on 12/Jul/18
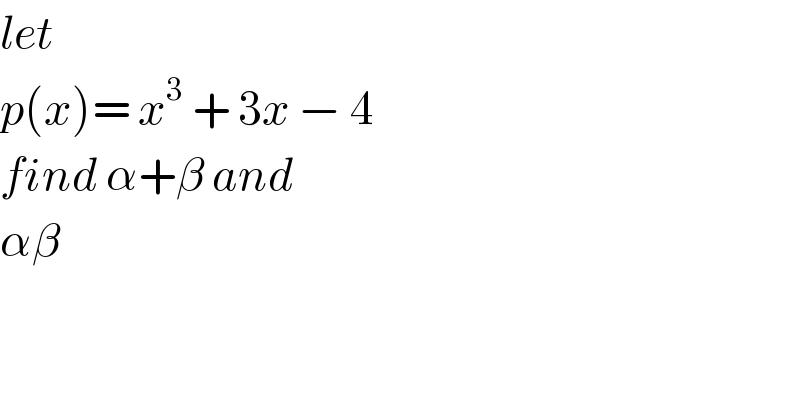
let p(x)= x^3 + 3x − 4 find α+β and αβ
letp(x)=x3+3x−4findα+βandαβ
Answered by MrW3 last updated on 12/Jul/18
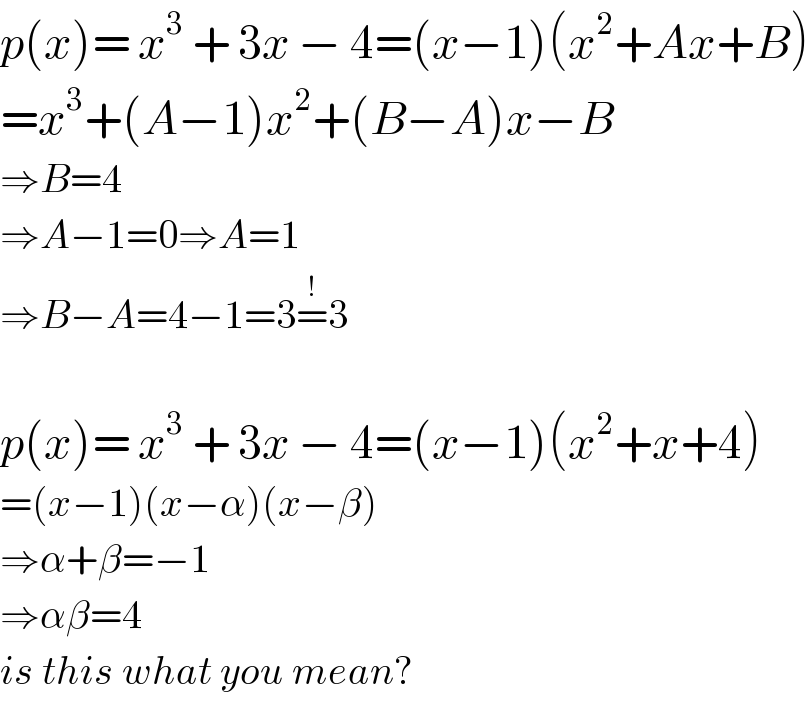
p(x)= x^3 + 3x − 4=(x−1)(x^2 +Ax+B) =x^3 +(A−1)x^2 +(B−A)x−B ⇒B=4 ⇒A−1=0⇒A=1 ⇒B−A=4−1=3=^! 3 p(x)= x^3 + 3x − 4=(x−1)(x^2 +x+4) =(x−1)(x−α)(x−β) ⇒α+β=−1 ⇒αβ=4 is this what you mean?
p(x)=x3+3x−4=(x−1)(x2+Ax+B)=x3+(A−1)x2+(B−A)x−B⇒B=4⇒A−1=0⇒A=1⇒B−A=4−1=3=!3p(x)=x3+3x−4=(x−1)(x2+x+4)=(x−1)(x−α)(x−β)⇒α+β=−1⇒αβ=4isthiswhatyoumean?
Answered by tanmay.chaudhury50@gmail.com last updated on 13/Jul/18
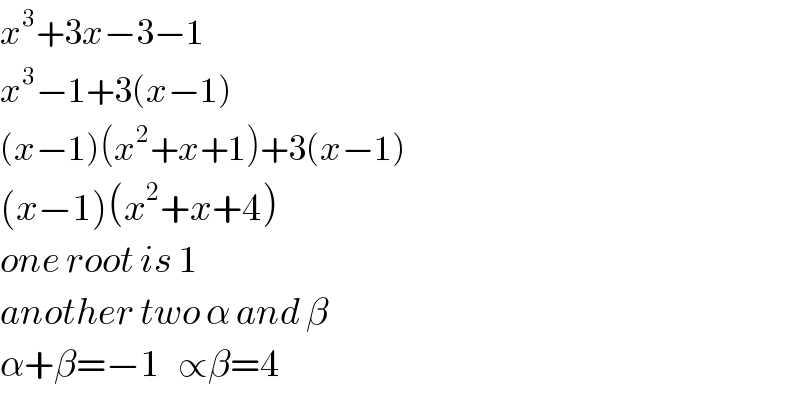
x^3 +3x−3−1 x^3 −1+3(x−1) (x−1)(x^2 +x+1)+3(x−1) (x−1)(x^2 +x+4) one root is 1 another two α and β α+β=−1 ∝β=4
x3+3x−3−1x3−1+3(x−1)(x−1)(x2+x+1)+3(x−1)(x−1)(x2+x+4)onerootis1anothertwoαandβα+β=−1∝β=4

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *