Question Number 26761 by abdo imad last updated on 29/Dec/17
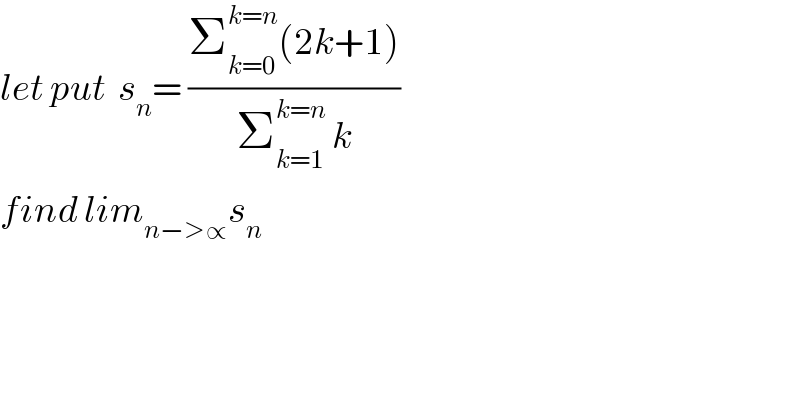
$${let}\:{put}\:\:{s}_{{n}} =\:\frac{\sum_{{k}=\mathrm{0}} ^{{k}={n}} \left(\mathrm{2}{k}+\mathrm{1}\right)}{\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:{k}} \\ $$$${find}\:{lim}_{{n}−>\propto} {s}_{{n}} \\ $$
Answered by prakash jain last updated on 29/Dec/17
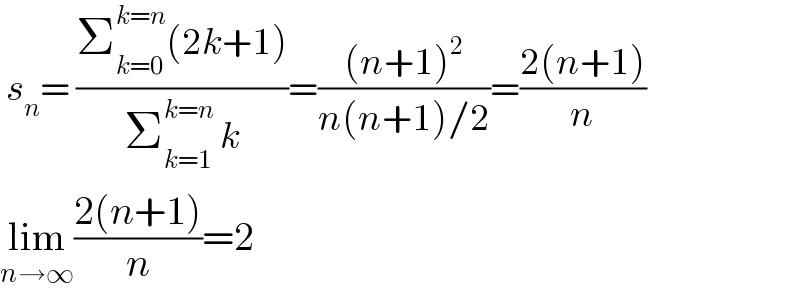
$$\:{s}_{{n}} =\:\frac{\sum_{{k}=\mathrm{0}} ^{{k}={n}} \left(\mathrm{2}{k}+\mathrm{1}\right)}{\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:{k}}=\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{{n}\left({n}+\mathrm{1}\right)/\mathrm{2}}=\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{{n}} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{2}\left({n}+\mathrm{1}\right)}{{n}}=\mathrm{2} \\ $$
Commented by abdo imad last updated on 29/Dec/17
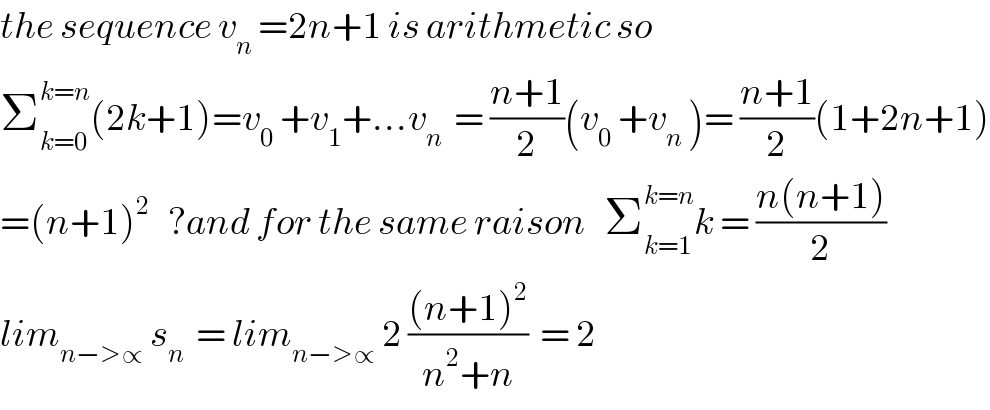
$${the}\:{sequence}\:{v}_{{n}} \:=\mathrm{2}{n}+\mathrm{1}\:{is}\:{arithmetic}\:{so} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{k}={n}} \left(\mathrm{2}{k}+\mathrm{1}\right)={v}_{\mathrm{0}} \:+{v}_{\mathrm{1}} +…{v}_{{n}} \:\:=\:\frac{{n}+\mathrm{1}}{\mathrm{2}}\left({v}_{\mathrm{0}} \:+{v}_{{n}} \:\right)=\:\frac{{n}+\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{2}{n}+\mathrm{1}\right) \\ $$$$=\left({n}+\mathrm{1}\right)^{\mathrm{2}} \:\:\:?{and}\:{for}\:{the}\:{same}\:{raison}\:\:\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} {k}\:=\:\frac{{n}\left({n}+\mathrm{1}\right)}{\mathrm{2}} \\ $$$${lim}_{{n}−>\propto} \:{s}_{{n}} \:\:=\:{lim}_{{n}−>\propto} \:\mathrm{2}\:\frac{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }{{n}^{\mathrm{2}} +{n}}\:\:=\:\mathrm{2} \\ $$
Commented by prakash jain last updated on 29/Dec/17

$$\mathrm{Thanks}.\:\mathrm{I}\:\mathrm{corrected}. \\ $$$$\mathrm{Earlier} \\ $$$$\underset{{i}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{2}{i}+\mathrm{1}\right)={n}^{\mathrm{2}} \:\left({it}\:{should}\:{have}\:{been}\right. \\ $$$$\left({n}+\mathrm{1}\right)^{\mathrm{2}} . \\ $$
