Question Number 26132 by abdo imad last updated on 21/Dec/17
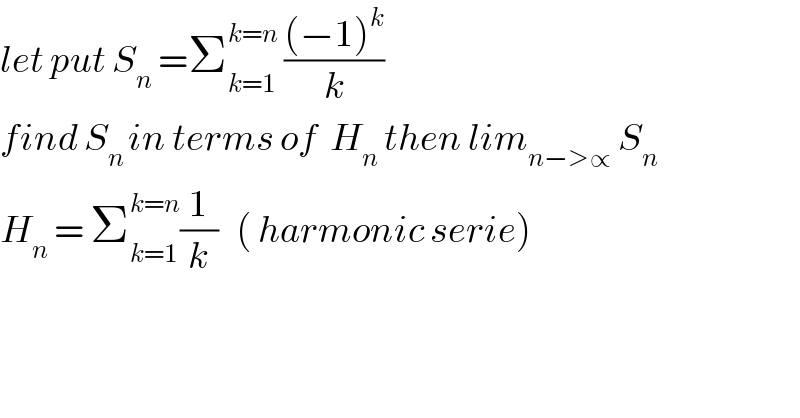
$${let}\:{put}\:{S}_{{n}} \:=\sum_{{k}=\mathrm{1}} ^{{k}={n}} \:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}} \\ $$$${find}\:{S}_{{n}\:} {in}\:{terms}\:{of}\:\:{H}_{{n}} \:{then}\:{lim}_{{n}−>\propto} \:{S}_{{n}} \\ $$$${H}_{{n}} \:=\:\sum_{{k}=\mathrm{1}} ^{{k}={n}} \frac{\mathrm{1}}{{k}}\:\:\:\left(\:{harmonic}\:{serie}\right) \\ $$
Commented by abdo imad last updated on 23/Dec/17
![S_n = Σ_(1≤k≤n_(k=2p) ) (((−1)^k )/k) + Σ_(1≤k≤n_(k=2p+1) ) (((−1)^k )/k) = Σ_(p=1) ^([ (n/2)]) (1/(2p)) − Σ_(p=0) ^([ ((n−1)/2)]) (1/(2p+1)) but Σ_(p=1) ^([(n/2)]) (1/(2p))= (1/2) H_([(n/2)]) and Σ_(p=0) ^([((n−1)/2)]) (1/(2p+1))=1+ (1/3) +(1/5) +...+ (1/(2[((n−1)/2)]+1)) =1 +(1/2) +(1/3)+ (1/4)+... +(1/(2[((n−1)/2)])) + (1/(2[((n−1)/2)]+1)) −(1/2) −(1/4) −...(1/(2[((n−1)/2)])) = H_(2[((n−1)/2)]+1) −(1/2) H_([((n−1)/2)]) ⇒ S_n = (1/2) H_([(n/2)]) + (1/2) H_([((n−1)/2)]) − H_(2[((n−1)/2)]+1) we have S_(2n) = (1/2) H_n + (1/2) H_(n−1) − H_(2n−1) but H_n = ln(n) +γ +o((1/n)) H_(n−1) = ln(n−1)+γ +o((1/n)) H_(2n−1) =ln(2n−1) +γ +o((1/n)) ⇒ S_(2n) = ln( (√(n(n−1)))) −ln(2n−1) +o((1/n)) =ln(((√(n(n−1)))/(2n−1)) ) +o( (( 1)/n)) ⇒ lim_(n−>∝) S_n =−ln(2) S_(2n+1) =(1/2) H_n + (1/2) H_n − H_(2n+1) =H_n − H_(2n+1) =ln((n/(2n+1))) +o((1/n)) ⇒ lim_(n−>∝) S_(2n+1) =−ln(2) finally lim_(n−>∝) S_n = −ln(2).](https://www.tinkutara.com/question/Q26305.png)
$${S}_{{n}} \:\:=\:\sum_{\mathrm{1}\leqslant{k}\leqslant{n}_{{k}=\mathrm{2}{p}} } \:\:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}}\:\:+\:\:\:\sum_{\mathrm{1}\leqslant{k}\leqslant{n}_{{k}=\mathrm{2}{p}+\mathrm{1}} } \:\:\frac{\left(−\mathrm{1}\right)^{{k}} }{{k}} \\ $$$$=\:\sum_{{p}=\mathrm{1}} ^{\left[\:\frac{{n}}{\mathrm{2}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{2}{p}}\:\:−\:\sum_{{p}=\mathrm{0}} ^{\left[\:\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{2}{p}+\mathrm{1}}\:\:{but}\:\:\sum_{{p}=\mathrm{1}} ^{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:\frac{\mathrm{1}}{\mathrm{2}{p}}=\:\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:{and} \\ $$$$\sum_{{p}=\mathrm{0}} ^{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\frac{\mathrm{1}}{\mathrm{2}{p}+\mathrm{1}}=\mathrm{1}+\:\frac{\mathrm{1}}{\mathrm{3}}\:\:+\frac{\mathrm{1}}{\mathrm{5}}\:+…+\:\:\frac{\mathrm{1}}{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}} \\ $$$$=\mathrm{1}\:+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}+\:\frac{\mathrm{1}}{\mathrm{4}}+…\:+\frac{\mathrm{1}}{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]}\:\:+\:\:\frac{\mathrm{1}}{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}}\:−\frac{\mathrm{1}}{\mathrm{4}}\:−…\frac{\mathrm{1}}{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \\ $$$$=\:{H}_{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}} \:\:\:−\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \\ $$$$ \\ $$$$\Rightarrow\:{S}_{{n}} \:\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{\left[\frac{{n}}{\mathrm{2}}\right]} \:\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]} \:\:−\:{H}_{\mathrm{2}\left[\frac{{n}−\mathrm{1}}{\mathrm{2}}\right]+\mathrm{1}} \\ $$$${we}\:{have}\:\:{S}_{\mathrm{2}{n}} =\:\:\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:+\:\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}−\mathrm{1}} −\:{H}_{\mathrm{2}{n}−\mathrm{1}} \\ $$$${but}\:\:{H}_{{n}} =\:{ln}\left({n}\right)\:+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$${H}_{{n}−\mathrm{1}} =\:{ln}\left({n}−\mathrm{1}\right)+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$${H}_{\mathrm{2}{n}−\mathrm{1}} \:={ln}\left(\mathrm{2}{n}−\mathrm{1}\right)\:+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$\Rightarrow\:\:{S}_{\mathrm{2}{n}} =\:{ln}\left(\:\sqrt{{n}\left({n}−\mathrm{1}\right)}\right)\:−{ln}\left(\mathrm{2}{n}−\mathrm{1}\right)\:+{o}\left(\frac{\mathrm{1}}{{n}}\right) \\ $$$$={ln}\left(\frac{\sqrt{{n}\left({n}−\mathrm{1}\right)}}{\mathrm{2}{n}−\mathrm{1}}\:\right)\:+{o}\left(\:\frac{\:\mathrm{1}}{{n}}\right)\:\:\:\Rightarrow\:\:\:{lim}_{{n}−>\propto} \:\:{S}_{{n}} \:\:=−{ln}\left(\mathrm{2}\right) \\ $$$${S}_{\mathrm{2}{n}+\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}\:\:{H}_{{n}} \:\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:{H}_{{n}} \:\:−\:{H}_{\mathrm{2}{n}+\mathrm{1}} \:={H}_{{n}} \:\:−\:{H}_{\mathrm{2}{n}+\mathrm{1}} \\ $$$$={ln}\left(\frac{{n}}{\mathrm{2}{n}+\mathrm{1}}\right)\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\:\:\:\Rightarrow\:\:{lim}_{{n}−>\propto} \:\:{S}_{\mathrm{2}{n}+\mathrm{1}} =−{ln}\left(\mathrm{2}\right) \\ $$$${finally}\:\:{lim}_{{n}−>\propto} \:\:{S}_{{n}} \:=\:−{ln}\left(\mathrm{2}\right). \\ $$
