Question Number 26243 by abdo imad last updated on 22/Dec/17
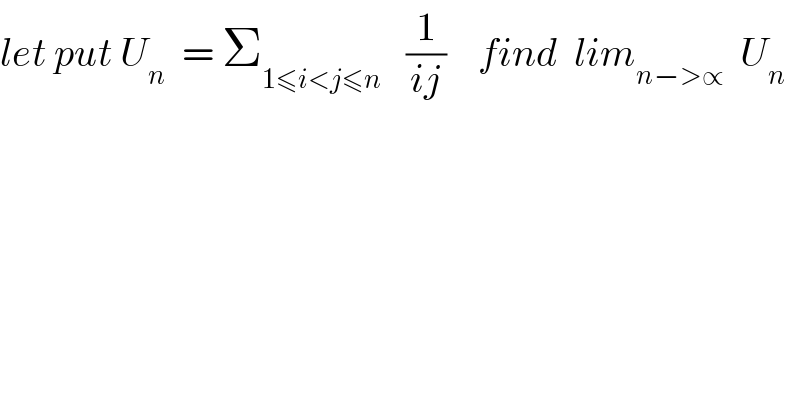
$${let}\:{put}\:{U}_{{n}} \:\:=\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\:\frac{\mathrm{1}}{{ij}}\:\:\:\:{find}\:\:{lim}_{{n}−>\propto} \:\:{U}_{{n}} \\ $$
Commented by abdo imad last updated on 28/Dec/17
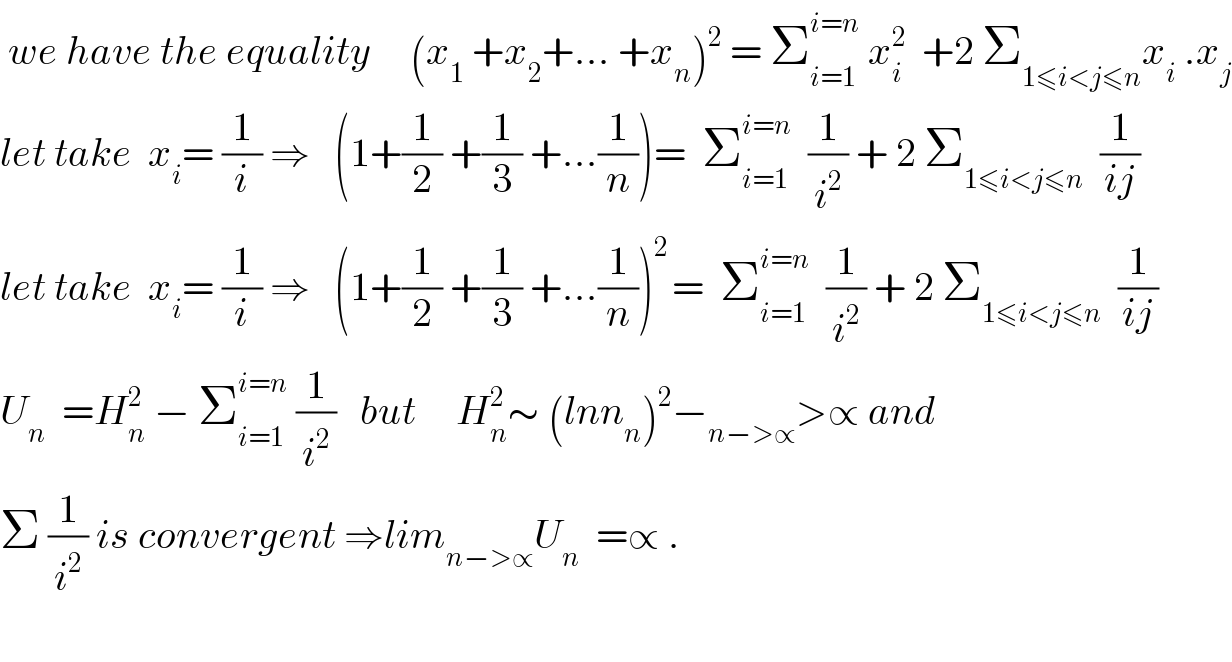
$$\:{we}\:{have}\:{the}\:{equality}\:\:\:\:\:\left({x}_{\mathrm{1}} \:+{x}_{\mathrm{2}} +…\:+{x}_{{n}} \right)^{\mathrm{2}} \:=\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:{x}_{{i}} ^{\mathrm{2}} \:\:+\mathrm{2}\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} {x}_{{i}} \:.{x}_{{j}} \\ $$$${let}\:{take}\:\:{x}_{{i}} =\:\frac{\mathrm{1}}{{i}}\:\Rightarrow\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+…\frac{\mathrm{1}}{{n}}\right)=\:\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:\:\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\:+\:\mathrm{2}\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\frac{\mathrm{1}}{{ij}} \\ $$$${let}\:{take}\:\:{x}_{{i}} =\:\frac{\mathrm{1}}{{i}}\:\Rightarrow\:\:\:\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{3}}\:+…\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}\:} =\:\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:\:\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\:+\:\mathrm{2}\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\frac{\mathrm{1}}{{ij}} \\ $$$${U}_{{n}} \:\:={H}_{{n}} ^{\mathrm{2}} \:−\:\sum_{{i}=\mathrm{1}} ^{{i}={n}} \:\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\:\:\:{but}\:\:\:\:\:{H}_{{n}} ^{\mathrm{2}} \sim\:\left({lnn}_{{n}} \right)^{\mathrm{2}} −_{{n}−>\propto} >\propto\:{and} \\ $$$$\Sigma\:\frac{\mathrm{1}}{{i}^{\mathrm{2}} }\:{is}\:{convergent}\:\Rightarrow{lim}_{{n}−>\propto} {U}_{{n}} \:\:=\propto\:. \\ $$$$ \\ $$
