let-R-and-a-n-k-1-n-sin-k-n-k-Find-lim-n-a-n-

Question Number 80332 by ~blr237~ last updated on 02/Feb/20

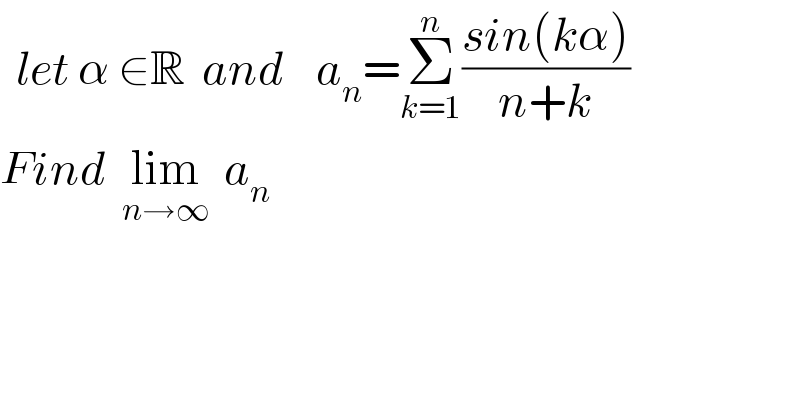
let α ∈R and a_n =Σ_(k=1) ^n ((sin(kα))/(n+k)) Find lim_(n→∞) a_n

$$\:\:{let}\:\alpha\:\in\mathbb{R}\:\:{and}\:\:\:\:{a}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{sin}\left({k}\alpha\right)}{{n}+{k}} \\ $$$${Find}\:\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\:{a}_{{n}} \: \\ $$

Commented by Rio Michael last updated on 03/Feb/20

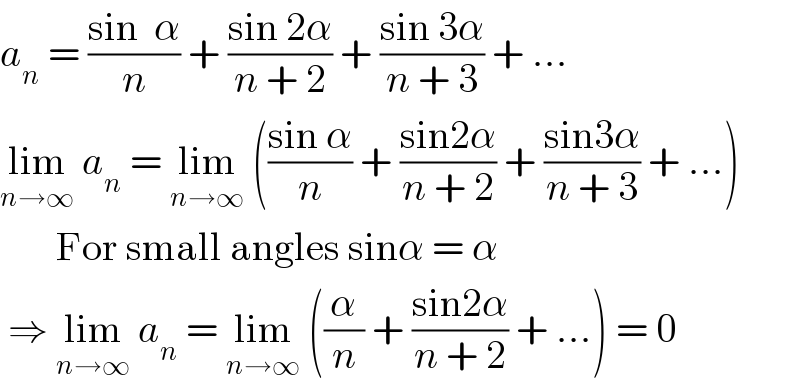
a_n = ((sin α)/n) + ((sin 2α)/(n + 2)) + ((sin 3α)/(n + 3)) + ... lim_(n→∞) a_n = lim_(n→∞) (((sin α)/n) + ((sin2α)/(n + 2)) + ((sin3α)/(n + 3)) + ...) For small angles sinα = α ⇒ lim_(n→∞) a_n = lim_(n→∞) ((α/n) + ((sin2α)/(n + 2)) + ...) = 0

$${a}_{{n}} \:=\:\frac{\mathrm{sin}\:\:\alpha}{{n}}\:+\:\frac{\mathrm{sin}\:\mathrm{2}\alpha}{{n}\:+\:\mathrm{2}}\:+\:\frac{\mathrm{sin}\:\mathrm{3}\alpha}{{n}\:+\:\mathrm{3}}\:+\:… \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} \:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\mathrm{sin}\:\alpha}{{n}}\:+\:\frac{\mathrm{sin2}\alpha}{{n}\:+\:\mathrm{2}}\:+\:\frac{\mathrm{sin3}\alpha}{{n}\:+\:\mathrm{3}}\:+\:…\right) \\ $$$$\:\:\:\:\:\:\:\mathrm{For}\:\mathrm{small}\:\mathrm{angles}\:\mathrm{sin}\alpha\:=\:\alpha \\ $$$$\:\Rightarrow\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{a}_{{n}} \:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left(\frac{\alpha}{{n}}\:+\:\frac{\mathrm{sin2}\alpha}{{n}\:+\:\mathrm{2}}\:+\:…\right)\:=\:\mathrm{0}\: \\ $$

Facebook Tweet Pin

let-R-and-a-n-k-1-n-sin-k-n-k-Find-lim-n-a-n-

Leave a Reply Cancel reply