Question Number 41517 by maxmathsup by imad last updated on 08/Aug/18
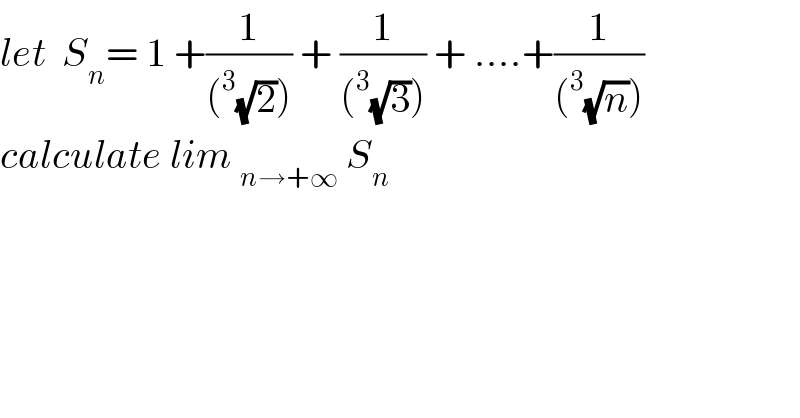
$${let}\:\:{S}_{{n}} =\:\mathrm{1}\:+\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{\mathrm{2}}\right)}\:+\:\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{\mathrm{3}}\right)}\:+\:….+\frac{\mathrm{1}}{\left(^{\mathrm{3}} \sqrt{{n}}\right)} \\ $$$${calculate}\:{lim}\:_{{n}\rightarrow+\infty} \:{S}_{{n}} \\ $$
Commented by maxmathsup by imad last updated on 10/Aug/18
![we have S_n =Σ_(k=1) ^n (1/k^(1/3) ) the function t→(1/x^(1/3) ) is decreasing so ∫_k ^(k+1) (dt/t^(1/3) ) ≤ (1/k^(1/3) ) ≤ ∫_(k−1) ^k (dt/t^(1/3) ) ⇒ Σ_(k=2) ^n ∫_k ^(k+1) (dt/t^(1/3) ) ≤ Σ_(k=2) ^n (1/k^(1/3) ) ≤ Σ_(k=2) ^n ∫_(k−1) ^k (dt/t^(1/3) ) ⇒ ∫_2 ^(n+1) t^(−(1/3)) dt ≤ S_n −1 ≤ ∫_1 ^n t^(−(1/3)) dt ⇒ [ (3/2) t^(2/3) ]_2 ^(n+1) ≤ S_n −1 ≤ [ (3/2) t^(2/3) ]_1 ^n ⇒(3/2){ (n+1)^(2/3) −2^(2/3) }≤ S_n −1 ≤ (3/2){ n^(2/3) −1}⇒ S_n ≥ 1 +(3/2)(n+1)^(2/3) −(3/2) 2^(2/3) →+∞(n→+∞) ⇒ lim_(n→+∞) S_n =+∞ .](https://www.tinkutara.com/question/Q41607.png)
$${we}\:{have}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{{k}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\:\:{the}\:{function}\:\:{t}\rightarrow\frac{\mathrm{1}}{{x}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:{is}\:{decreasing}\:{so}\: \\ $$$$\:\int_{{k}} ^{{k}+\mathrm{1}} \:\:\frac{{dt}}{{t}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\leqslant\:\:\:\frac{\mathrm{1}}{{k}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\leqslant\:\:\int_{{k}−\mathrm{1}} ^{{k}} \:\:\frac{{dt}}{{t}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\Rightarrow\:\sum_{{k}=\mathrm{2}} ^{{n}} \:\:\int_{{k}} ^{{k}+\mathrm{1}} \:\frac{{dt}}{{t}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\leqslant\:\sum_{{k}=\mathrm{2}} ^{{n}} \:\:\frac{\mathrm{1}}{{k}^{\frac{\mathrm{1}}{\mathrm{3}}} }\:\leqslant\:\sum_{{k}=\mathrm{2}} ^{{n}} \:\int_{{k}−\mathrm{1}} ^{{k}} \:\:\frac{{dt}}{{t}^{\frac{\mathrm{1}}{\mathrm{3}}} } \\ $$$$\Rightarrow\:\:\int_{\mathrm{2}} ^{{n}+\mathrm{1}} \:\:{t}^{−\frac{\mathrm{1}}{\mathrm{3}}} \:{dt}\:\leqslant\:\:{S}_{{n}} −\mathrm{1}\:\leqslant\:\:\int_{\mathrm{1}} ^{{n}} \:\:\:{t}^{−\frac{\mathrm{1}}{\mathrm{3}}} \:{dt}\:\Rightarrow \\ $$$$\left[\:\:\frac{\mathrm{3}}{\mathrm{2}}\:{t}^{\frac{\mathrm{2}}{\mathrm{3}}} \right]_{\mathrm{2}} ^{{n}+\mathrm{1}} \:\leqslant\:{S}_{{n}} −\mathrm{1}\:\leqslant\:\left[\:\frac{\mathrm{3}}{\mathrm{2}}\:{t}^{\frac{\mathrm{2}}{\mathrm{3}}} \right]_{\mathrm{1}} ^{{n}} \:\Rightarrow\frac{\mathrm{3}}{\mathrm{2}}\left\{\:\left({n}+\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:−\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} \right\}\leqslant\:{S}_{{n}} −\mathrm{1} \\ $$$$\leqslant\:\frac{\mathrm{3}}{\mathrm{2}}\left\{\:\:{n}^{\frac{\mathrm{2}}{\mathrm{3}}} \:−\mathrm{1}\right\}\Rightarrow\:{S}_{{n}} \:\geqslant\:\mathrm{1}\:+\frac{\mathrm{3}}{\mathrm{2}}\left({n}+\mathrm{1}\right)^{\frac{\mathrm{2}}{\mathrm{3}}} \:−\frac{\mathrm{3}}{\mathrm{2}}\:\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} \:\rightarrow+\infty\left({n}\rightarrow+\infty\right)\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} =+\infty\:. \\ $$
Answered by alex041103 last updated on 09/Aug/18
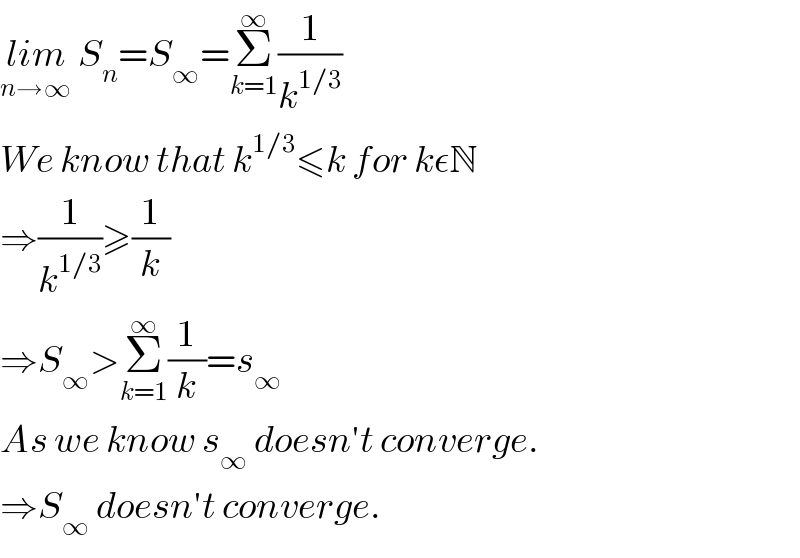
$$\underset{{n}\rightarrow\infty} {{lim}}\:{S}_{{n}} ={S}_{\infty} =\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{\mathrm{1}/\mathrm{3}} } \\ $$$${We}\:{know}\:{that}\:{k}^{\mathrm{1}/\mathrm{3}} \leqslant{k}\:{for}\:{k}\epsilon\mathbb{N} \\ $$$$\Rightarrow\frac{\mathrm{1}}{{k}^{\mathrm{1}/\mathrm{3}} }\geqslant\frac{\mathrm{1}}{{k}} \\ $$$$\Rightarrow{S}_{\infty} >\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}}={s}_{\infty} \\ $$$${As}\:{we}\:{know}\:{s}_{\infty} \:{doesn}'{t}\:{converge}. \\ $$$$\Rightarrow{S}_{\infty} \:{doesn}'{t}\:{converge}. \\ $$
