let-S-n-k-1-1-k-1-k-and-T-n-k-1-1-k-1-2k-1-1-calculate-lim-S-n-and-lim-T-n-n-2-prove-that-S-n-ln2-and-T-n-pi-4-converges-and-find-its-sum-

Tinku Tara June 4, 2023 Relation and Functions 0 Comments

Question Number 33348 by caravan msup abdo. last updated on 14/Apr/18

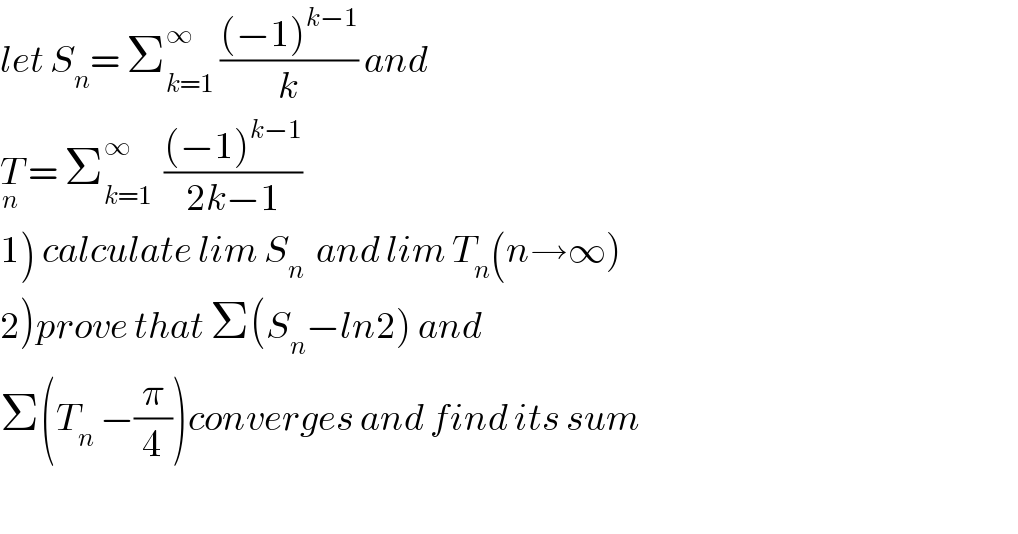
let S_n = Σ_(k=1) ^∞ (((−1)^(k−1) )/k) and T_n = Σ_(k=1) ^∞ (((−1)^(k−1) )/(2k−1)) 1) calculate lim S_n and lim T_n (n→∞) 2)prove that Σ(S_n −ln2) and Σ(T_n −(π/4))converges and find its sum

$${let}\:{S}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{{k}}\:{and} \\ $$$$\underset{{n}} {{T}}\:=\:\sum_{{k}=\mathrm{1}} ^{\infty} \:\:\frac{\left(−\mathrm{1}\right)^{{k}−\mathrm{1}} }{\mathrm{2}{k}−\mathrm{1}} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{lim}\:{S}_{{n}} \:\:{and}\:{lim}\:{T}_{{n}} \left({n}\rightarrow\infty\right) \\ $$$$\left.\mathrm{2}\right){prove}\:{that}\:\Sigma\left({S}_{{n}} −{ln}\mathrm{2}\right)\:{and} \\ $$$$\Sigma\left({T}_{{n}} \:−\frac{\pi}{\mathrm{4}}\right){converges}\:{and}\:{find}\:{its}\:{sum} \\ $$$$ \\ $$

Facebook Tweet Pin

let-S-n-k-1-1-k-1-k-and-T-n-k-1-1-k-1-2k-1-1-calculate-lim-S-n-and-lim-T-n-n-2-prove-that-S-n-ln2-and-T-n-pi-4-converges-and-find-its-sum-

Leave a Reply Cancel reply