Question Number 43546 by maxmathsup by imad last updated on 11/Sep/18
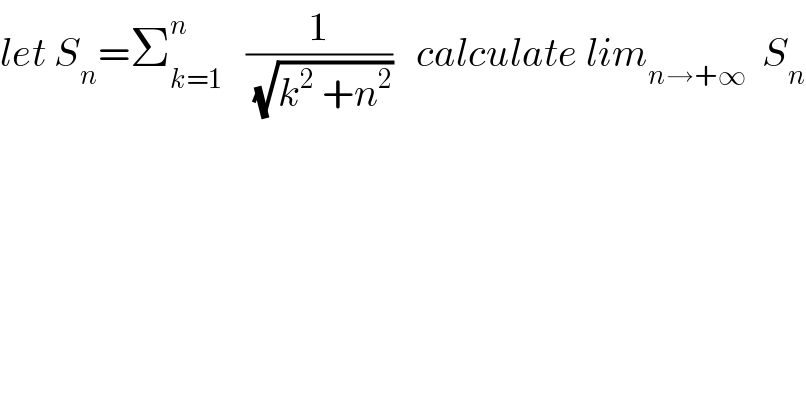
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\:\frac{\mathrm{1}}{\:\sqrt{{k}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }}\:\:\:{calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:{S}_{{n}} \\ $$
Answered by behi83417@gmail.com last updated on 12/Sep/18

$${S}_{{n}} =\sum_{\mathrm{1}} ^{{n}} \frac{\mathrm{1}}{{n}}.\frac{\mathrm{1}}{\:\sqrt{\mathrm{1}+\left(\frac{{k}}{{n}}\right)^{\mathrm{2}} }}=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}= \\ $$$$={ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)_{\mathrm{0}} ^{\mathrm{1}} ={ln}\left(\sqrt{\mathrm{2}}+\mathrm{1}\right). \\ $$
Commented by maxmathsup by imad last updated on 12/Sep/18
![cha7gement x =tanθ give ∫_0 ^1 (dx/( (√(1+x^2 )))) =∫_0 ^(π/4) ((1+tan^2 θ)/( (√(1+tan^2 θ))))dθ = ∫_0 ^(π/4) (√(1+tan^2 θ))= ∫_0 ^(π/4) (dθ/(cosθ)) =_(tan((θ/2))=u) ∫_0 ^((√2)−1) (1/((1−t^2 )/(1+t^2 ))) ((2du)/(1+u^2 )) = ∫_0 ^((√2)−1) {(1/(1−u)) +(1/(1+u))}du =[ln∣((1+u)/(1−u))∣]_0 ^((√2)−1) =ln∣ ((√2)/(2−(√2)))∣ =ln((1/( (√2)−1)))=ln(1+(√2)) ⇒lim_(n→+∞) S_n =ln(1+(√2)) another way ∫_0 ^1 (dx/( (√(1+x^2 )))) =[argsh(x)]_0 ^1 =[ln(x+(√(1+x^2 )))]_0 ^1 =ln(1+(√2)).](https://www.tinkutara.com/question/Q43594.png)
$${cha}\mathrm{7}{gement}\:{x}\:={tan}\theta\:{give}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\:\frac{\mathrm{1}+{tan}^{\mathrm{2}} \theta}{\:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}}{d}\theta \\ $$$$=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\sqrt{\mathrm{1}+{tan}^{\mathrm{2}} \theta}=\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \:\frac{{d}\theta}{{cos}\theta}\:=_{{tan}\left(\frac{\theta}{\mathrm{2}}\right)={u}} \:\:\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\:\frac{\mathrm{1}}{\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} } \\ $$$$=\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:\:\left\{\frac{\mathrm{1}}{\mathrm{1}−{u}}\:+\frac{\mathrm{1}}{\mathrm{1}+{u}}\right\}{du}\:=\left[{ln}\mid\frac{\mathrm{1}+{u}}{\mathrm{1}−{u}}\mid\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}−\mathrm{1}} \:={ln}\mid\:\frac{\sqrt{\mathrm{2}}}{\mathrm{2}−\sqrt{\mathrm{2}}}\mid \\ $$$$={ln}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}−\mathrm{1}}\right)={ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} ={ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\: \\ $$$${another}\:{way}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}\:=\left[{argsh}\left({x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:=\left[{ln}\left({x}+\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:={ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right). \\ $$
