Question Number 129872 by Bird last updated on 20/Jan/21
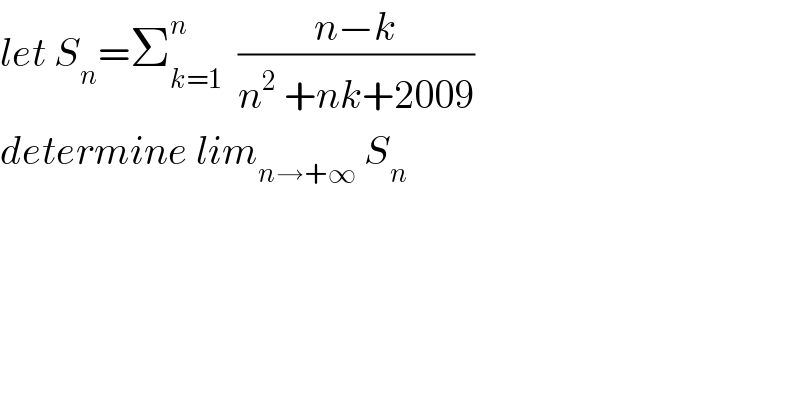
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{{n}−{k}}{{n}^{\mathrm{2}} \:+{nk}+\mathrm{2009}} \\ $$$${determine}\:{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} \\ $$
Answered by Dwaipayan Shikari last updated on 20/Jan/21
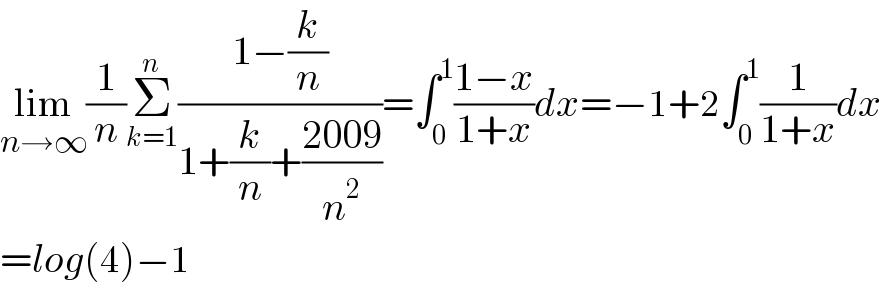
$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}−\frac{{k}}{{n}}}{\mathrm{1}+\frac{{k}}{{n}}+\frac{\mathrm{2009}}{{n}^{\mathrm{2}} }}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}−{x}}{\mathrm{1}+{x}}{dx}=−\mathrm{1}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{1}+{x}}{dx} \\ $$$$={log}\left(\mathrm{4}\right)−\mathrm{1} \\ $$
Commented by mathmax by abdo last updated on 20/Jan/21
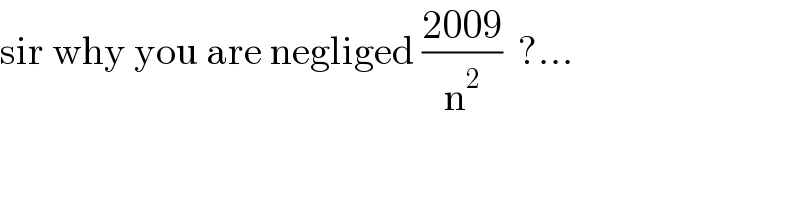
$$\mathrm{sir}\:\mathrm{why}\:\mathrm{you}\:\mathrm{are}\:\mathrm{negliged}\:\frac{\mathrm{2009}}{\mathrm{n}^{\mathrm{2}} }\:\:?… \\ $$
