let-S-n-p-k-0-n-k-p-prove-that-S-n-p-1-p-1-n-1-p-1-k-0-n-1-C-p-1-k-S-n-k-

Tinku Tara June 4, 2023 Relation and Functions 0 Comments

Question Number 52669 by maxmathsup by imad last updated on 11/Jan/19

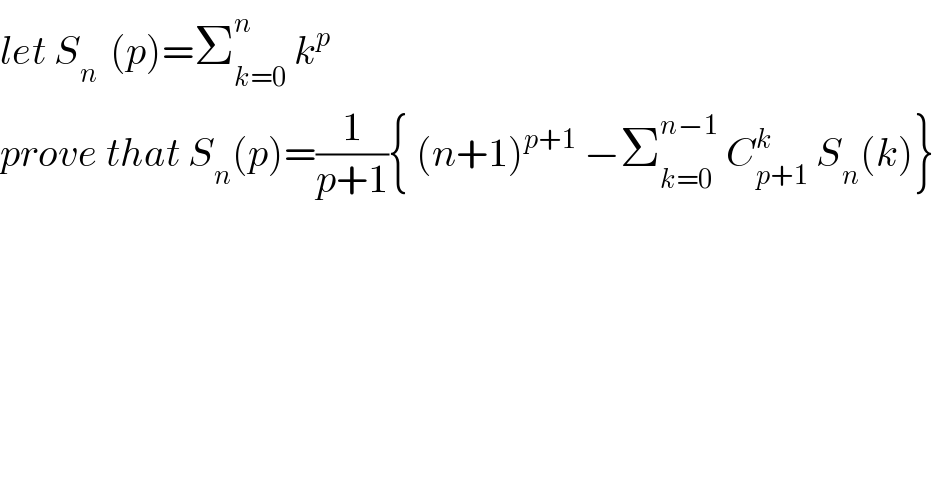
let S_(n ) (p)=Σ_(k=0) ^n k^p prove that S_n (p)=(1/(p+1)){ (n+1)^(p+1) −Σ_(k=0) ^(n−1) C_(p+1) ^k S_n (k)}

$${let}\:{S}_{{n}\:} \:\left({p}\right)=\sum_{{k}=\mathrm{0}} ^{{n}} \:{k}^{{p}} \\ $$$${prove}\:{that}\:{S}_{{n}} \left({p}\right)=\frac{\mathrm{1}}{{p}+\mathrm{1}}\left\{\:\left({n}+\mathrm{1}\right)^{{p}+\mathrm{1}} \:−\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{C}_{{p}+\mathrm{1}} ^{{k}} \:{S}_{{n}} \left({k}\right)\right\} \\ $$

Facebook Tweet Pin

let-S-n-p-k-0-n-k-p-prove-that-S-n-p-1-p-1-n-1-p-1-k-0-n-1-C-p-1-k-S-n-k-

Leave a Reply Cancel reply