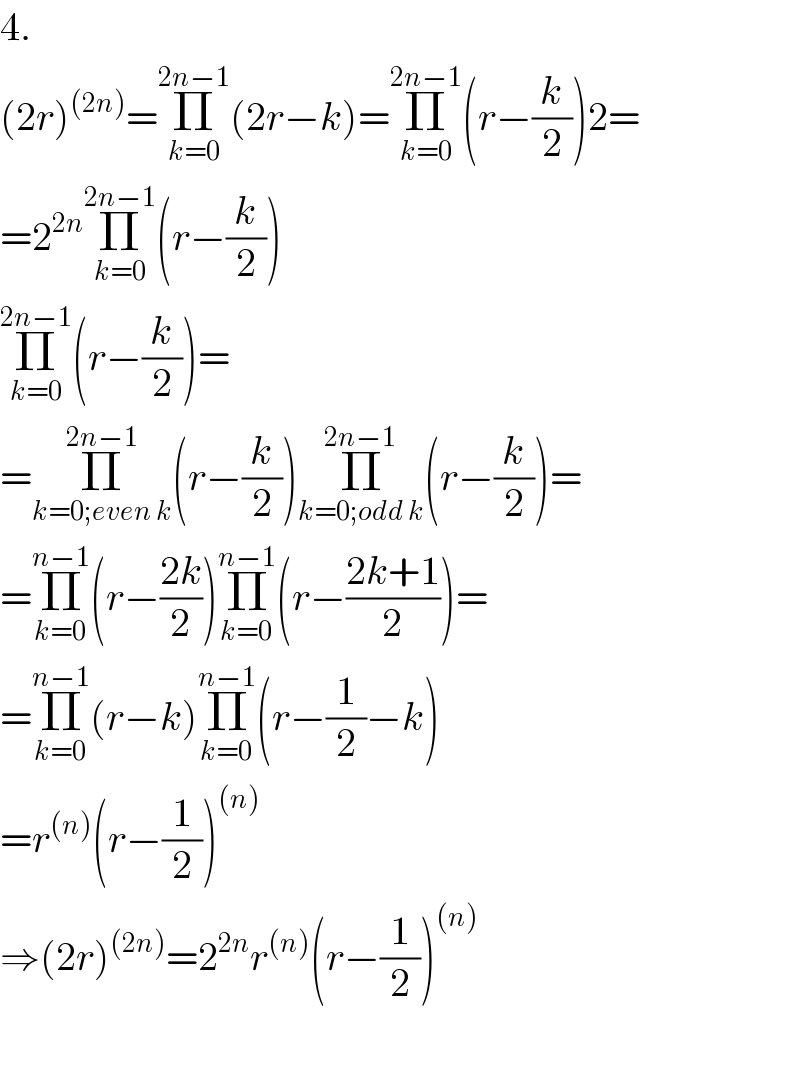Question Number 115534 by Hassen_Timol last updated on 26/Sep/20
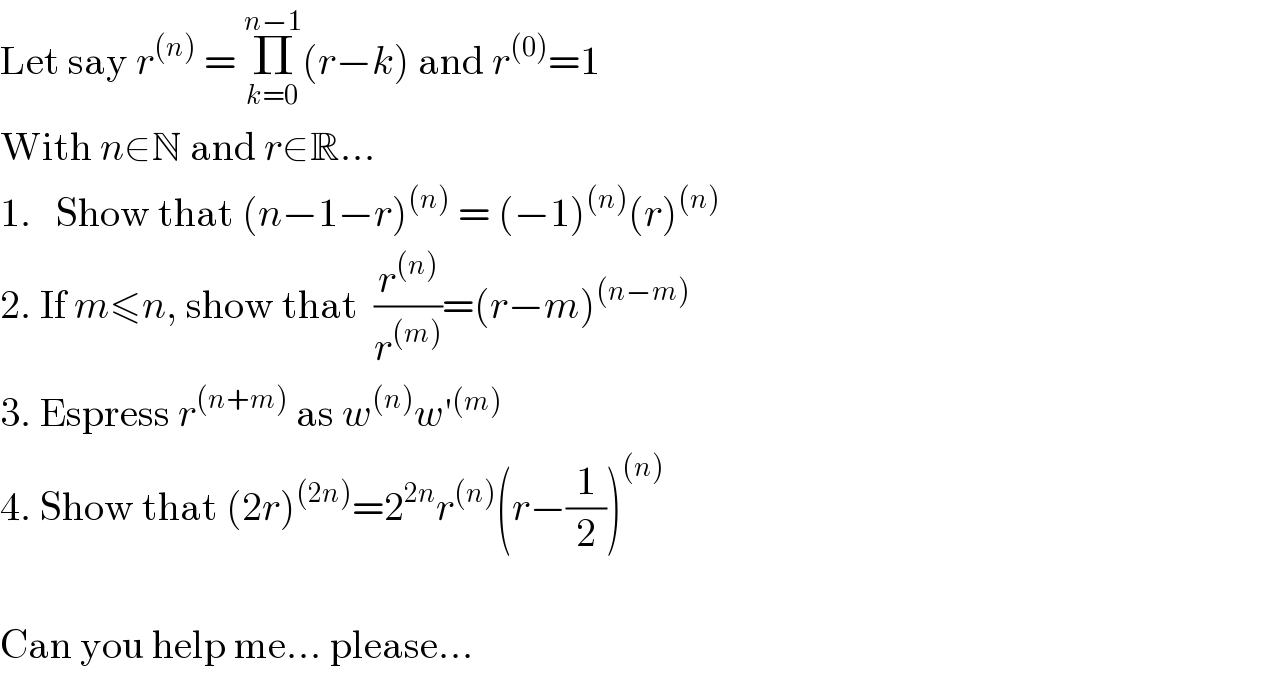
Commented by Hassen_Timol last updated on 26/Sep/20
Answered by aleks041103 last updated on 26/Sep/20
![1. (n−1−r)^((n)) =Π_(k=0) ^(n−1) (n−1−r−k)= =Π_(k=0) ^(n−1) ((n−1−k)−r) let i=n−1−k, so if k∈[0,n−1] then i∈[n−1,0]≡[0,n−1] Π_(k=0) ^(n−1) ((n−1−k)−r)=Π_(i=0) ^(n−1) (i−r)= =Π_(i=0) ^(n−1) (r−i)(−1)=Π_(i=0) ^(n−1) (r−i)Π_(i=0) ^(n−1) (−1)= =r^((n)) (−1)^n ⇒(n−1−r)^((n)) =(−1)^n r^((n))](https://www.tinkutara.com/question/Q115580.png)
Commented by Hassen_Timol last updated on 26/Sep/20
Thank you so much, it's very nice ! thanks a lot... if you know how to do for the other questions, it would be even more nice ! But once again, thanks a lot
Commented by aleks041103 last updated on 27/Sep/20
Answered by aleks041103 last updated on 26/Sep/20
![2. (r^((n)) /r^((m)) )=((Π_(k=0) ^(n−1) (r−k))/(Π_(k=0) ^(m−1) (r−k)))=((Π_(k=0) ^(m−1) (r−k)Π_(k=m) ^(n−1) (r−k))/(Π_(k=0) ^(m−1) (r−k))) =Π_(k=m) ^(n−1) (r−k) let k=m+i, so if k∈[m,n−1] then i∈[0,(n−m)−1] (r^((n)) /r^((m)) )=Π_(i=0) ^((n−m)−1) (r−(m+i))= =Π_(i=0) ^((n−m)−1) ((r−m)−i)=(r−m)^((n−m)) ⇒(r^((n)) /r^((m)) )=(r−m)^((n−m))](https://www.tinkutara.com/question/Q115586.png)
Commented by Hassen_Timol last updated on 26/Sep/20
Thank you very much !
Answered by aleks041103 last updated on 27/Sep/20
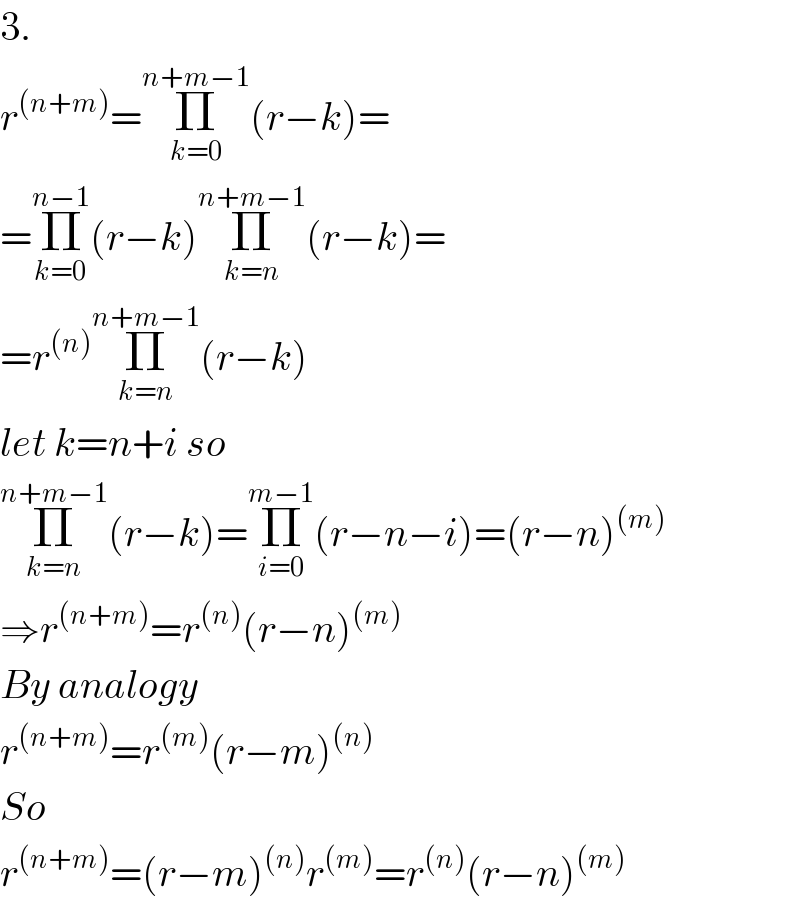
Answered by aleks041103 last updated on 27/Sep/20