Question Number 181125 by depressiveshrek last updated on 21/Nov/22

$${Let}\:{the}\:{acute}\:{triangle}\:\Delta{ABC}\:\:{have} \\ $$$${an}\:{outer}\:{circumscribed}\:{circle}, \\ $$$${whose}\:{tangents}\:{at}\:{the}\:{points}\:{B}\:{and}\:{C} \\ $$$${intersect}\:{at}\:{point}\:{P}.\:{Let}\:{D}\:{and}\:{E}\:{be} \\ $$$${the}\:{projections}\:{of}\:{perpendicular} \\ $$$${lines}\:{from}\:{point}\:{P}\:{on}\:{AC}\:{and}\:{AB}. \\ $$$${Prove}\:{that}\:{the}\:{interdection}\:{point}\:{of} \\ $$$${the}\:{heights}\:{of}\:\Delta{ADE}\:{is}\:{the}\:{midpoint} \\ $$$${of}\:{BC} \\ $$
Commented by mr W last updated on 22/Nov/22
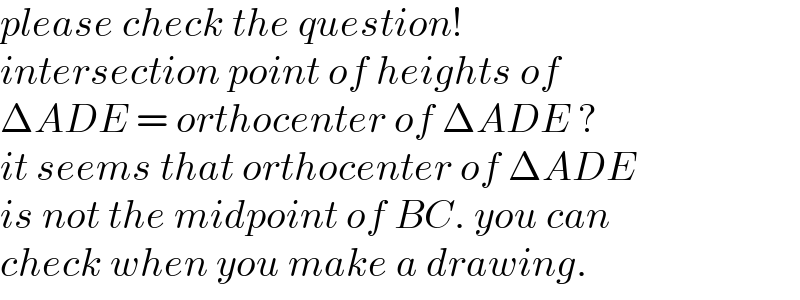
$${please}\:{check}\:{the}\:{question}! \\ $$$${intersection}\:{point}\:{of}\:{heights}\:{of} \\ $$$$\Delta{ADE}\:=\:{orthocenter}\:{of}\:\Delta{ADE}\:? \\ $$$${it}\:{seems}\:{that}\:{orthocenter}\:{of}\:\Delta{ADE} \\ $$$${is}\:{not}\:{the}\:{midpoint}\:{of}\:{BC}.\:{you}\:{can} \\ $$$${check}\:{when}\:{you}\:{make}\:{a}\:{drawing}. \\ $$
Commented by depressiveshrek last updated on 22/Nov/22

$${I}\:{also}\:{find}\:{the}\:{question}\:{to}\:{be}\:{confusing}, \\ $$$${the}\:{intersection}\:{is}\:{clearly}\:{not}\:{the} \\ $$$${midpoint}\:{of}\:{BC} \\ $$
Commented by mr W last updated on 22/Nov/22
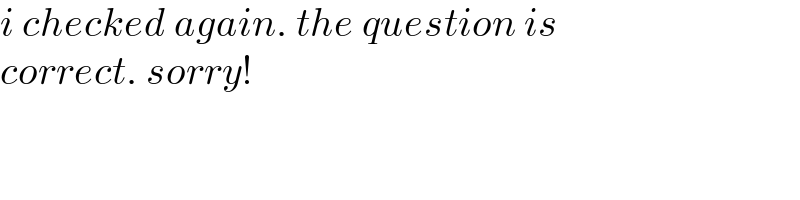
$${i}\:{checked}\:{again}.\:{the}\:{question}\:{is} \\ $$$${correct}.\:{sorry}! \\ $$
Answered by mr W last updated on 22/Nov/22