Menu Close

Let-the-points-P-x-n-1-y-n-1-Q-x-n-y-n-and-R-x-n-1-y-n-1-lies-on-the-curve-y-f-x-Prove-that-y-n-1-y-n-1-2h-dy-dx-n-

Tinku Tara 0 Comments
Pin




Question Number 122187 by physicstutes last updated on 14/Nov/20
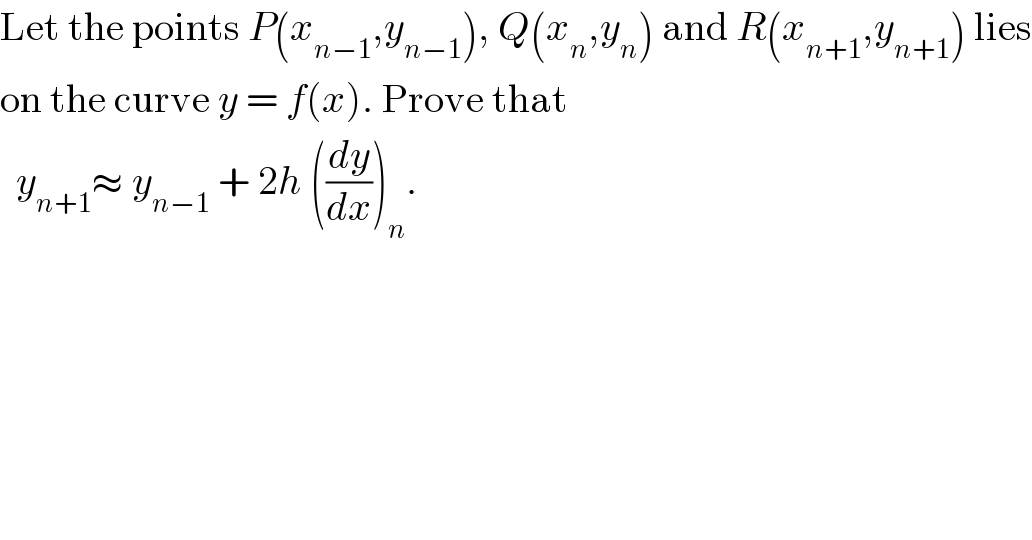
Let the points P(x_(n−1) ,y_(n−1) ), Q(x_n ,y_n ) and R(x_(n+1) ,y_(n+1) ) lies on the curve y = f(x). Prove that y_(n+1) ≈ y_(n−1) + 2h ((dy/dx))_n .
$$\mathrm{Let}\:\mathrm{the}\:\mathrm{points}\:{P}\left({x}_{{n}−\mathrm{1}} ,{y}_{{n}−\mathrm{1}} \right),\:{Q}\left({x}_{{n}} ,{y}_{{n}} \right)\:\mathrm{and}\:{R}\left({x}_{{n}+\mathrm{1}} ,{y}_{{n}+\mathrm{1}} \right)\:\mathrm{lies} \\ $$$$\mathrm{on}\:\mathrm{the}\:\mathrm{curve}\:{y}\:=\:{f}\left({x}\right).\:\mathrm{Prove}\:\mathrm{that}\: \\ $$$$\:\:{y}_{{n}+\mathrm{1}} \approx\:{y}_{{n}−\mathrm{1}} \:+\:\mathrm{2}{h}\:\left(\frac{{dy}}{{dx}}\right)_{{n}} .\: \\ $$
Answered by Olaf last updated on 14/Nov/20
{ ((((dy/dx))_n ≈ ((y_n −y_(n−1) )/(x_n −x_(n−1) )) (1))),((((dy/dx))_n ≈ ((y_(n+1) −y_n )/(x_(n+1) −x_n ))(2))) :} { ((((dy/dx))_n ≈ ((y_n −y_(n−1) )/h) (1))),((((dy/dx))_n ≈ ((y_(n+1) −y_n )/h) (2))) :} (1)+(2) : 2((dy/dx))_n ≈ ((y_(n+1) −y_(n−1) )/h) ⇒ y_(n+1) ≈ y_(n−1) +2h((dy/dx))_n
$$\begin{cases}{\left(\frac{{dy}}{{dx}}\right)_{{n}} \:\approx\:\frac{{y}_{{n}} −{y}_{{n}−\mathrm{1}} }{{x}_{{n}} −{x}_{{n}−\mathrm{1}} }\:\left(\mathrm{1}\right)}\\{\left(\frac{{dy}}{{dx}}\right)_{{n}} \:\approx\:\frac{{y}_{{n}+\mathrm{1}} −{y}_{{n}} }{{x}_{{n}+\mathrm{1}} −{x}_{{n}} }\left(\mathrm{2}\right)}\end{cases} \\ $$$$\begin{cases}{\left(\frac{{dy}}{{dx}}\right)_{{n}} \:\approx\:\frac{{y}_{{n}} −{y}_{{n}−\mathrm{1}} }{{h}}\:\left(\mathrm{1}\right)}\\{\left(\frac{{dy}}{{dx}}\right)_{{n}} \:\approx\:\frac{{y}_{{n}+\mathrm{1}} −{y}_{{n}} }{{h}}\:\left(\mathrm{2}\right)}\end{cases} \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{2}\right)\:: \\ $$$$\mathrm{2}\left(\frac{{dy}}{{dx}}\right)_{{n}} \:\approx\:\frac{{y}_{{n}+\mathrm{1}} −{y}_{{n}−\mathrm{1}} }{{h}} \\ $$$$\Rightarrow\:{y}_{{n}+\mathrm{1}} \:\approx\:{y}_{{n}−\mathrm{1}} +\mathrm{2}{h}\left(\frac{{dy}}{{dx}}\right)_{{n}} \\ $$
Commented by physicstutes last updated on 14/Nov/20
Thank you sir... What if i do this: Assuming P → 0 , R → 0 such that we can approximate f(x) to a straight line. then; ((dy/dx))_n ≈ ((y_(n+1) −y_(n−1) )/(x_(n+1) −x_(n−1) )) where x_(n+1) −x_(n−1) = x_(n+1) −x_n + x_n −x_(n−1) = 2h ⇒ ((dy/dx))_n ≈ ((y_(n+1) −y_(n−1) )/(2h)) ⇒ y_(n+1) ≈ y_(n−1) + 2h((dy/dx))_n Is my approxation (P→0,R→0) worth it?
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}… \\ $$$$\mathrm{What}\:\mathrm{if}\:\mathrm{i}\:\mathrm{do}\:\mathrm{this}: \\ $$$$\:\mathrm{Assuming}\:{P}\:\rightarrow\:\mathrm{0}\:,\:{R}\:\rightarrow\:\mathrm{0}\:\mathrm{such}\:\mathrm{that}\:\mathrm{we}\:\mathrm{can}\:\mathrm{approximate} \\ $$$${f}\left({x}\right)\:\mathrm{to}\:\mathrm{a}\:\mathrm{straight}\:\mathrm{line}. \\ $$$$\mathrm{then};\:\:\left(\frac{{dy}}{{dx}}\right)_{{n}} \approx\:\frac{{y}_{{n}+\mathrm{1}} −{y}_{{n}−\mathrm{1}} }{{x}_{{n}+\mathrm{1}} −{x}_{{n}−\mathrm{1}} } \\ $$$$\mathrm{where}\:{x}_{{n}+\mathrm{1}} −{x}_{{n}−\mathrm{1}} \:=\:{x}_{{n}+\mathrm{1}} −{x}_{{n}} \:+\:{x}_{{n}} −{x}_{{n}−\mathrm{1}} \:=\:\mathrm{2}{h} \\ $$$$\Rightarrow\:\left(\frac{{dy}}{{dx}}\right)_{{n}} \approx\:\frac{{y}_{{n}+\mathrm{1}} −{y}_{{n}−\mathrm{1}} }{\mathrm{2}{h}} \\ $$$$\Rightarrow\:\:{y}_{{n}+\mathrm{1}} \:\approx\:{y}_{{n}−\mathrm{1}} \:+\:\mathrm{2}{h}\left(\frac{{dy}}{{dx}}\right)_{{n}} \\ $$$$\mathrm{Is}\:\mathrm{my}\:\mathrm{approxation}\:\left({P}\rightarrow\mathrm{0},{R}\rightarrow\mathrm{0}\right)\:\mathrm{worth}\:\mathrm{it}? \\ $$
Commented by Olaf last updated on 14/Nov/20
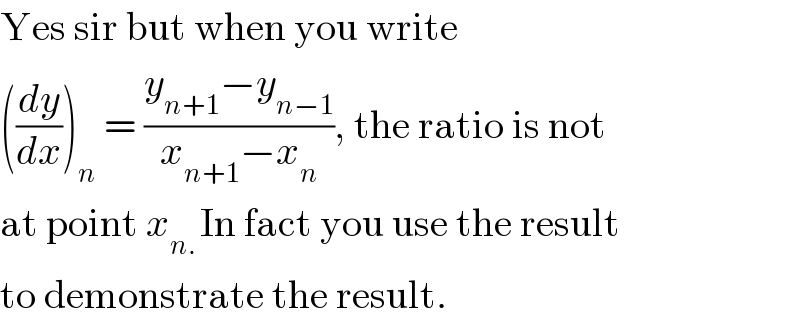
Yes sir but when you write ((dy/dx))_n = ((y_(n+1) −y_(n−1) )/(x_(n+1) −x_n )), the ratio is not at point x_(n. ) In fact you use the result to demonstrate the result.
$$\mathrm{Yes}\:\mathrm{sir}\:\mathrm{but}\:\mathrm{when}\:\mathrm{you}\:\mathrm{write}\: \\ $$$$\left(\frac{{dy}}{{dx}}\right)_{{n}} \:=\:\frac{{y}_{{n}+\mathrm{1}} −{y}_{{n}−\mathrm{1}} }{{x}_{{n}+\mathrm{1}} −{x}_{{n}} },\:\mathrm{the}\:\mathrm{ratio}\:\mathrm{is}\:\mathrm{not} \\ $$$$\mathrm{at}\:\mathrm{point}\:{x}_{{n}.\:} \mathrm{In}\:\mathrm{fact}\:\mathrm{you}\:\mathrm{use}\:\mathrm{the}\:\mathrm{result} \\ $$$$\mathrm{to}\:\mathrm{demonstrate}\:\mathrm{the}\:\mathrm{result}. \\ $$
Commented by physicstutes last updated on 14/Nov/20
Actually i write, ((dy/dx))_n ≈ ((y_(n+1) −y_(n−1) )/(x_(n+1) −x_(n−1) )) considering the points P(x_(n−1) ,y_(n−1) ) and R(x_(n+1) ,y_(n+1) ) Now i used the idea that, the step length (or x−differences) is h so the idea is x_(n+1) −x_n = x_n −x_(n−1) = h ⇒ x_(n+1) −x_(n−1) = x_(n+1) −x_n + x_n −x_(n−1) = 2h This happens when we solve differential equations numerical. so does this makes more sense?
$$\mathrm{Actually}\:\mathrm{i}\:\mathrm{write}, \\ $$$$\:\:\left(\frac{{dy}}{{dx}}\right)_{{n}} \approx\:\frac{{y}_{{n}+\mathrm{1}} −{y}_{{n}−\mathrm{1}} }{{x}_{{n}+\mathrm{1}} −{x}_{{n}−\mathrm{1}} }\:\: \\ $$$$\mathrm{considering}\:\mathrm{the}\:\mathrm{points}\:{P}\left({x}_{{n}−\mathrm{1}} ,{y}_{{n}−\mathrm{1}} \:\right)\:\mathrm{and}\:{R}\left({x}_{{n}+\mathrm{1}} ,{y}_{{n}+\mathrm{1}} \right) \\ $$$$\mathrm{Now}\:\mathrm{i}\:\mathrm{used}\:\mathrm{the}\:\mathrm{idea}\:\mathrm{that},\:\mathrm{the}\:\mathrm{step}\:\mathrm{length}\:\left(\mathrm{or}\:\mathrm{x}−\mathrm{differences}\right)\:\mathrm{is}\:{h} \\ $$$$\mathrm{so}\:\mathrm{the}\:\mathrm{idea}\:\mathrm{is}\:{x}_{{n}+\mathrm{1}} −{x}_{{n}} \:=\:{x}_{{n}} −{x}_{{n}−\mathrm{1}} \:=\:{h} \\ $$$$\Rightarrow\:{x}_{{n}+\mathrm{1}} −{x}_{{n}−\mathrm{1}} =\:{x}_{{n}+\mathrm{1}} −{x}_{{n}} \:+\:{x}_{{n}} −{x}_{{n}−\mathrm{1}} \:=\:\mathrm{2}{h} \\ $$$$\mathrm{This}\:\mathrm{happens}\:\mathrm{when}\:\mathrm{we}\:\mathrm{solve}\:\mathrm{differential}\:\mathrm{equations}\:\mathrm{numerical}. \\ $$$$\mathrm{so}\:\mathrm{does}\:\mathrm{this}\:\mathrm{makes}\:\mathrm{more}\:\mathrm{sense}? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *