Question Number 42789 by maxmathsup by imad last updated on 02/Sep/18
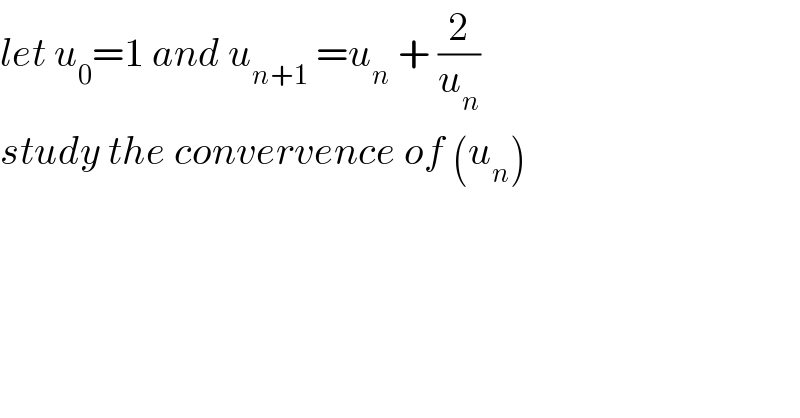
$${let}\:{u}_{\mathrm{0}} =\mathrm{1}\:{and}\:{u}_{{n}+\mathrm{1}} \:={u}_{{n}} \:+\:\frac{\mathrm{2}}{{u}_{{n}} } \\ $$$${study}\:{the}\:{convervence}\:{of}\:\left({u}_{{n}} \right) \\ $$
Commented by maxmathsup by imad last updated on 30/Sep/18
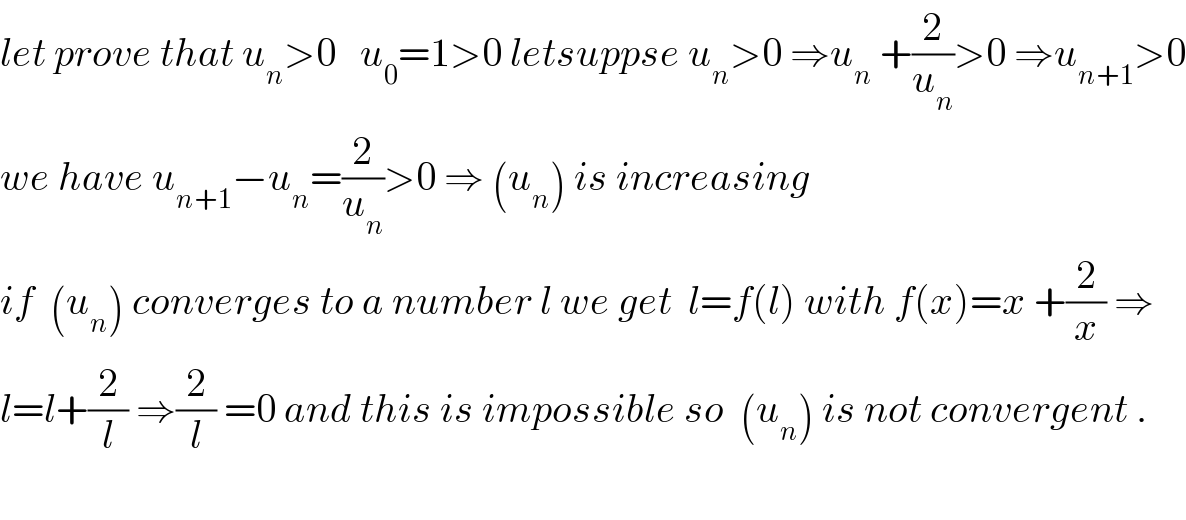
$${let}\:{prove}\:{that}\:{u}_{{n}} >\mathrm{0}\:\:\:{u}_{\mathrm{0}} =\mathrm{1}>\mathrm{0}\:{letsuppse}\:{u}_{{n}} >\mathrm{0}\:\Rightarrow{u}_{{n}} \:+\frac{\mathrm{2}}{{u}_{{n}} }>\mathrm{0}\:\Rightarrow{u}_{{n}+\mathrm{1}} >\mathrm{0} \\ $$$${we}\:{have}\:{u}_{{n}+\mathrm{1}} −{u}_{{n}} =\frac{\mathrm{2}}{{u}_{{n}} }>\mathrm{0}\:\Rightarrow\:\left({u}_{{n}} \right)\:{is}\:{increasing} \\ $$$${if}\:\:\left({u}_{{n}} \right)\:{converges}\:{to}\:{a}\:{number}\:{l}\:{we}\:{get}\:\:{l}={f}\left({l}\right)\:{with}\:{f}\left({x}\right)={x}\:+\frac{\mathrm{2}}{{x}}\:\Rightarrow \\ $$$${l}={l}+\frac{\mathrm{2}}{{l}}\:\Rightarrow\frac{\mathrm{2}}{{l}}\:=\mathrm{0}\:{and}\:{this}\:{is}\:{impossible}\:{so}\:\:\left({u}_{{n}} \right)\:{is}\:{not}\:{convergent}\:. \\ $$$$ \\ $$
