Question Number 32293 by abdo imad last updated on 22/Mar/18
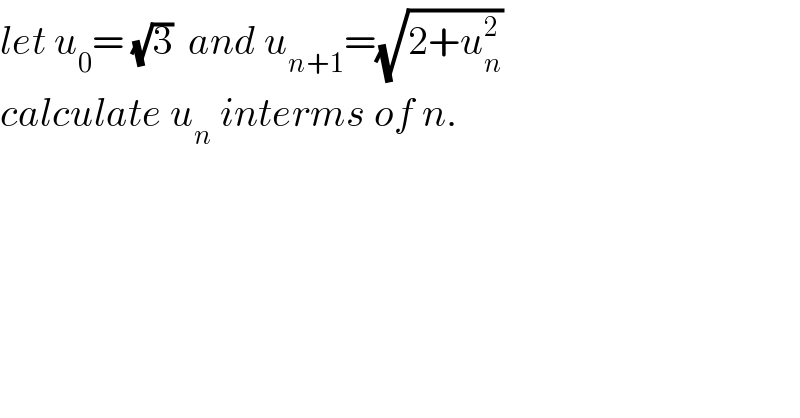
$${let}\:{u}_{\mathrm{0}} =\:\sqrt{\mathrm{3}}\:\:{and}\:{u}_{{n}+\mathrm{1}} =\sqrt{\mathrm{2}+{u}_{{n}} ^{\mathrm{2}} } \\ $$$${calculate}\:{u}_{{n}} \:{interms}\:{of}\:{n}. \\ $$
Commented by abdo imad last updated on 24/Mar/18
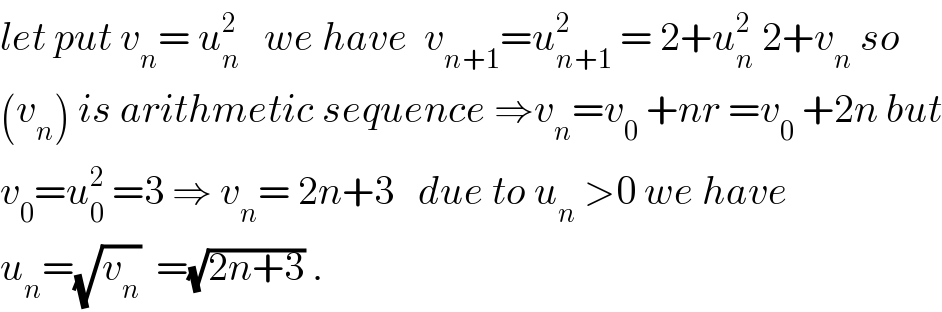
$${let}\:{put}\:{v}_{{n}} =\:{u}_{{n}} ^{\mathrm{2}} \:\:\:{we}\:{have}\:\:{v}_{{n}+\mathrm{1}} ={u}_{{n}+\mathrm{1}} ^{\mathrm{2}} \:=\:\mathrm{2}+{u}_{{n}} ^{\mathrm{2}} \:\mathrm{2}+{v}_{{n}} \:{so} \\ $$$$\left({v}_{{n}} \right)\:{is}\:{arithmetic}\:{sequence}\:\Rightarrow{v}_{{n}} ={v}_{\mathrm{0}} \:+{nr}\:={v}_{\mathrm{0}} \:+\mathrm{2}{n}\:{but} \\ $$$${v}_{\mathrm{0}} ={u}_{\mathrm{0}} ^{\mathrm{2}} \:=\mathrm{3}\:\Rightarrow\:{v}_{{n}} =\:\mathrm{2}{n}+\mathrm{3}\:\:\:{due}\:{to}\:{u}_{{n}} \:>\mathrm{0}\:{we}\:{have} \\ $$$${u}_{{n}} =\sqrt{{v}_{{n}} }\:\:=\sqrt{\mathrm{2}{n}+\mathrm{3}}\:. \\ $$
Answered by mrW2 last updated on 24/Mar/18
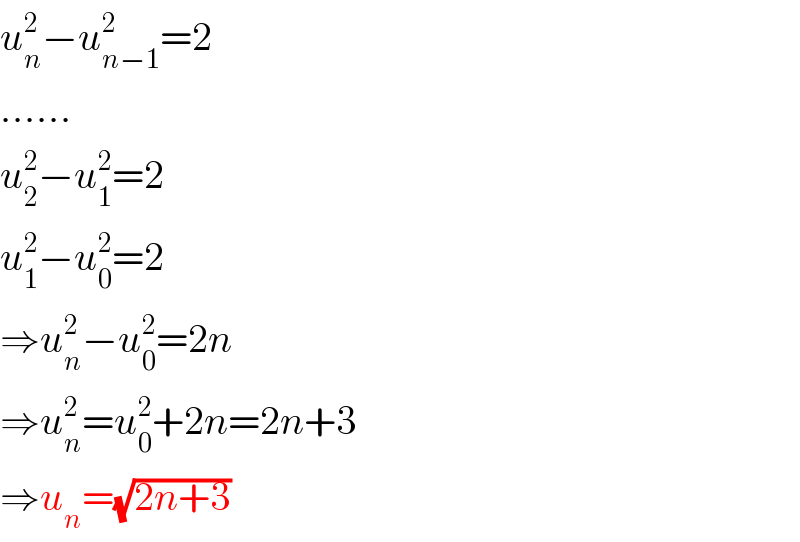
$${u}_{{n}} ^{\mathrm{2}} −{u}_{{n}−\mathrm{1}} ^{\mathrm{2}} =\mathrm{2} \\ $$$$…… \\ $$$${u}_{\mathrm{2}} ^{\mathrm{2}} −{u}_{\mathrm{1}} ^{\mathrm{2}} =\mathrm{2} \\ $$$${u}_{\mathrm{1}} ^{\mathrm{2}} −{u}_{\mathrm{0}} ^{\mathrm{2}} =\mathrm{2} \\ $$$$\Rightarrow{u}_{{n}} ^{\mathrm{2}} −{u}_{\mathrm{0}} ^{\mathrm{2}} =\mathrm{2}{n} \\ $$$$\Rightarrow{u}_{{n}} ^{\mathrm{2}} ={u}_{\mathrm{0}} ^{\mathrm{2}} +\mathrm{2}{n}=\mathrm{2}{n}+\mathrm{3} \\ $$$$\Rightarrow{u}_{{n}} =\sqrt{\mathrm{2}{n}+\mathrm{3}} \\ $$
Commented by abdo imad last updated on 24/Mar/18
$${your}\:{answer}\:{is}\:{correct}\:{sir}\:{thanks}… \\ $$
