Question Number 50392 by Abdo msup. last updated on 16/Dec/18
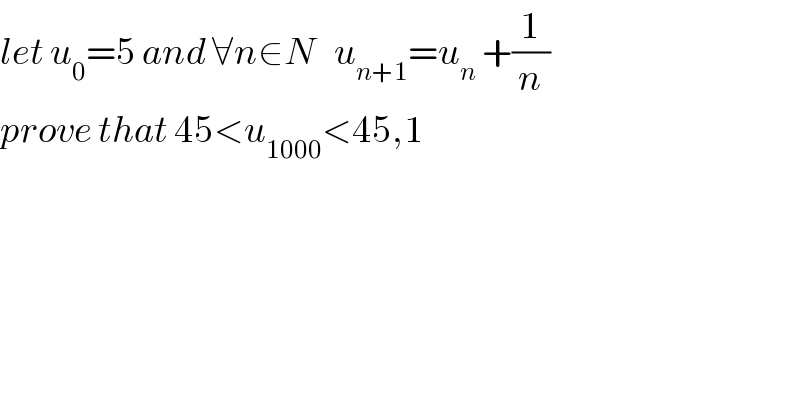
$${let}\:{u}_{\mathrm{0}} =\mathrm{5}\:{and}\:\forall{n}\in{N}\:\:\:{u}_{{n}+\mathrm{1}} ={u}_{{n}} \:+\frac{\mathrm{1}}{{n}} \\ $$$${prove}\:{that}\:\mathrm{45}<{u}_{\mathrm{1000}} <\mathrm{45},\mathrm{1} \\ $$
