Question Number 43541 by abdo.msup.com last updated on 11/Sep/18
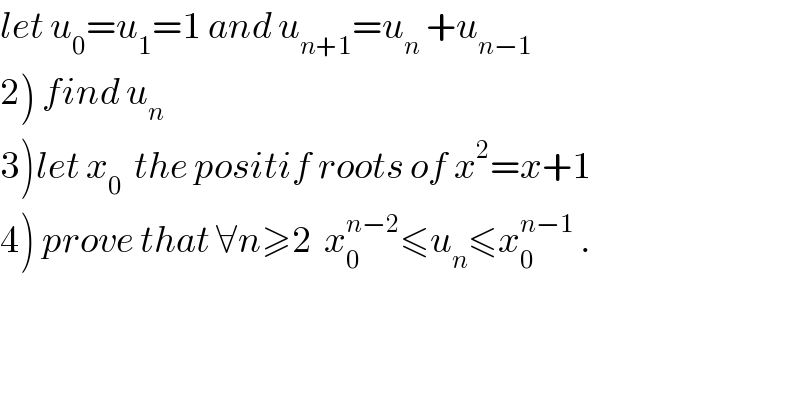
$${let}\:{u}_{\mathrm{0}} ={u}_{\mathrm{1}} =\mathrm{1}\:{and}\:{u}_{{n}+\mathrm{1}} ={u}_{{n}} \:+{u}_{{n}−\mathrm{1}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{u}_{{n}} \\ $$$$\left.\mathrm{3}\right){let}\:{x}_{\mathrm{0}} \:\:{the}\:{positif}\:{roots}\:{of}\:{x}^{\mathrm{2}} ={x}+\mathrm{1} \\ $$$$\left.\mathrm{4}\right)\:{prove}\:{that}\:\forall{n}\geqslant\mathrm{2}\:\:{x}_{\mathrm{0}} ^{{n}−\mathrm{2}} \leqslant{u}_{{n}} \leqslant{x}_{\mathrm{0}} ^{{n}−\mathrm{1}} \:. \\ $$
Answered by behi83417@gmail.com last updated on 12/Sep/18
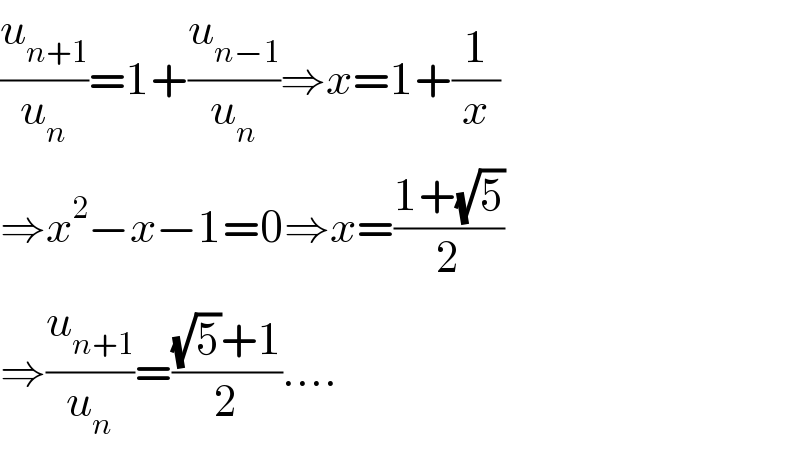
$$\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }=\mathrm{1}+\frac{{u}_{{n}−\mathrm{1}} }{{u}_{{n}} }\Rightarrow{x}=\mathrm{1}+\frac{\mathrm{1}}{{x}} \\ $$$$\Rightarrow{x}^{\mathrm{2}} −{x}−\mathrm{1}=\mathrm{0}\Rightarrow{x}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow\frac{{u}_{{n}+\mathrm{1}} }{{u}_{{n}} }=\frac{\sqrt{\mathrm{5}}+\mathrm{1}}{\mathrm{2}}…. \\ $$
