Question Number 53464 by maxmathsup by imad last updated on 22/Jan/19
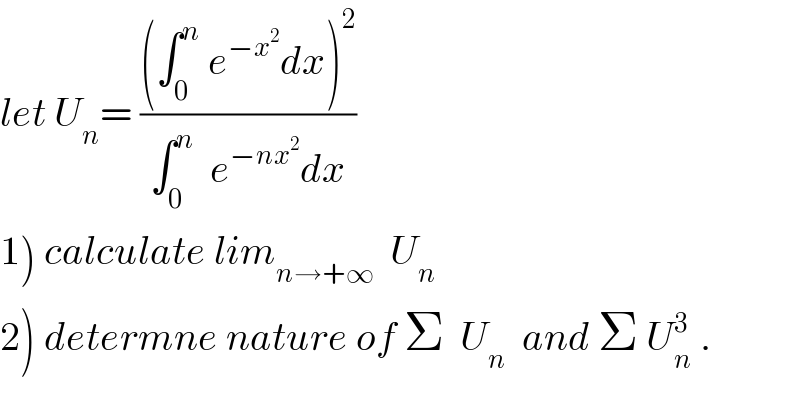
$${let}\:{U}_{{n}} =\:\frac{\left(\int_{\mathrm{0}} ^{{n}} \:{e}^{−{x}^{\mathrm{2}} } {dx}\right)^{\mathrm{2}} }{\int_{\mathrm{0}} ^{{n}} \:\:{e}^{−{nx}^{\mathrm{2}} } {dx}} \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{lim}_{{n}\rightarrow+\infty} \:\:{U}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{determne}\:{nature}\:{of}\:\Sigma\:\:{U}_{{n}} \:\:{and}\:\Sigma\:{U}_{{n}} ^{\mathrm{3}} \:. \\ $$
Commented by maxmathsup by imad last updated on 24/Jan/19
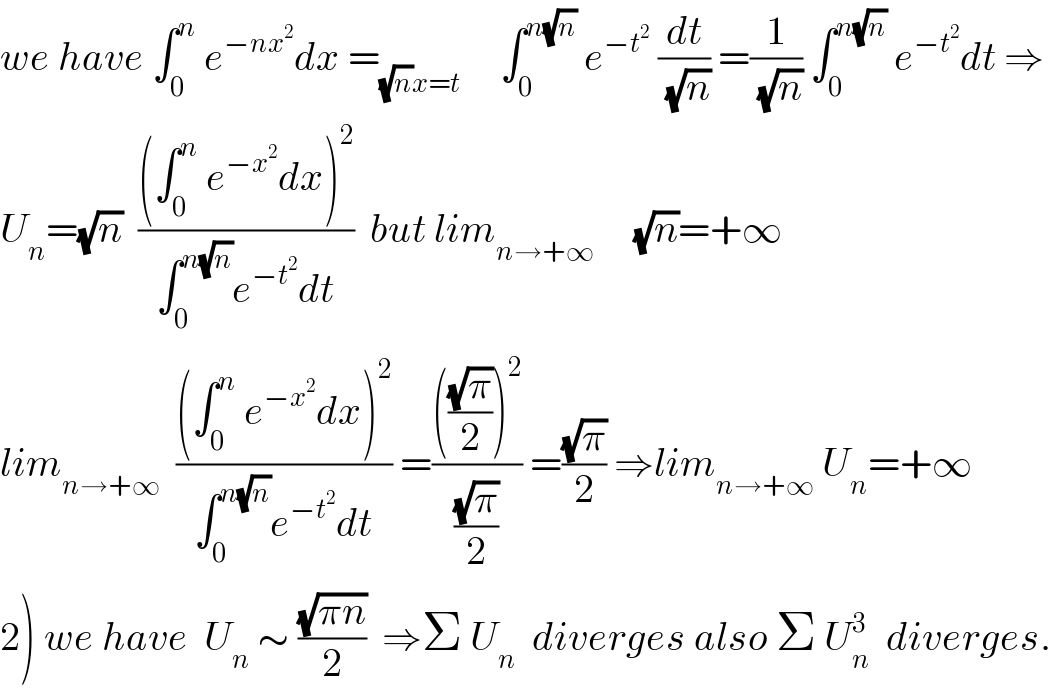
$${we}\:{have}\:\int_{\mathrm{0}} ^{{n}} \:{e}^{−{nx}^{\mathrm{2}} } {dx}\:=_{\sqrt{{n}}{x}={t}} \:\:\:\:\:\int_{\mathrm{0}} ^{{n}\sqrt{{n}}} \:{e}^{−{t}^{\mathrm{2}} } \:\frac{{dt}}{\:\sqrt{{n}}}\:=\frac{\mathrm{1}}{\:\sqrt{{n}}}\:\int_{\mathrm{0}} ^{{n}\sqrt{{n}}} \:{e}^{−{t}^{\mathrm{2}} } {dt}\:\Rightarrow \\ $$$${U}_{{n}} =\sqrt{{n}}\:\:\frac{\left(\int_{\mathrm{0}} ^{{n}} \:{e}^{−{x}^{\mathrm{2}} } {dx}\right)^{\mathrm{2}} }{\int_{\mathrm{0}} ^{{n}\sqrt{{n}}} {e}^{−{t}^{\mathrm{2}} } {dt}}\:\:{but}\:{lim}_{{n}\rightarrow+\infty} \:\:\:\:\:\sqrt{{n}}=+\infty \\ $$$${lim}_{{n}\rightarrow+\infty} \:\:\frac{\left(\int_{\mathrm{0}} ^{{n}} \:{e}^{−{x}^{\mathrm{2}} } {dx}\right)^{\mathrm{2}} }{\int_{\mathrm{0}} ^{{n}\sqrt{{n}}} {e}^{−{t}^{\mathrm{2}} } {dt}}\:=\frac{\left(\frac{\sqrt{\pi}}{\mathrm{2}}\right)^{\mathrm{2}} }{\frac{\sqrt{\pi}}{\mathrm{2}}}\:=\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{U}_{{n}} =+\infty \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:\:{U}_{{n}} \:\sim\:\frac{\sqrt{\pi{n}}}{\mathrm{2}}\:\:\Rightarrow\Sigma\:{U}_{{n}} \:\:{diverges}\:{also}\:\Sigma\:{U}_{{n}} ^{\mathrm{3}} \:\:{diverges}. \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 22/Jan/19
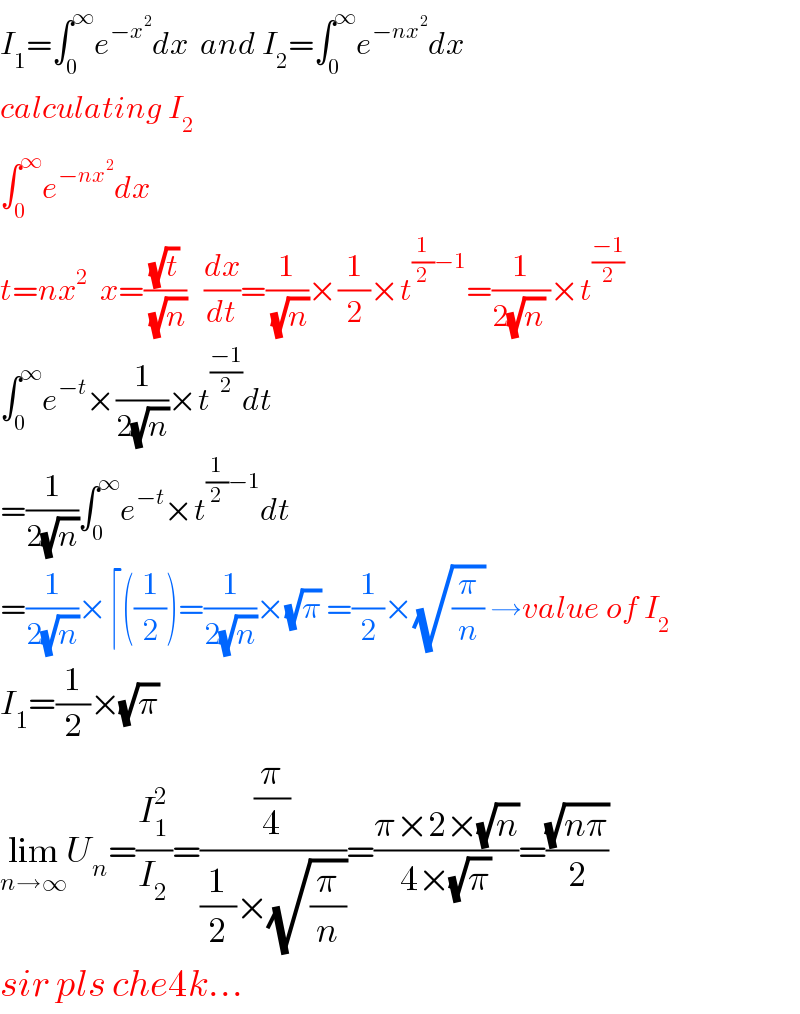
$${I}_{\mathrm{1}} =\int_{\mathrm{0}} ^{\infty} {e}^{−{x}^{\mathrm{2}} } {dx}\:\:{and}\:{I}_{\mathrm{2}} =\int_{\mathrm{0}} ^{\infty} {e}^{−{nx}^{\mathrm{2}} } {dx} \\ $$$${calculating}\:{I}_{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{nx}^{\mathrm{2}} } {dx} \\ $$$${t}={nx}^{\mathrm{2}} \:\:{x}=\frac{\sqrt{{t}}}{\:\sqrt{{n}}}\:\:\:\frac{{dx}}{{dt}}=\frac{\mathrm{1}}{\:\sqrt{{n}}}×\frac{\mathrm{1}}{\mathrm{2}}×{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}\:}×{t}^{\frac{−\mathrm{1}}{\mathrm{2}}} \\ $$$$\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} ×\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}×{t}^{\frac{−\mathrm{1}}{\mathrm{2}}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}\int_{\mathrm{0}} ^{\infty} {e}^{−{t}} ×{t}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}×\lceil\left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\frac{\mathrm{1}}{\mathrm{2}\sqrt{{n}}}×\sqrt{\pi}\:=\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\frac{\pi}{{n}}}\:\rightarrow{value}\:{of}\:{I}_{\mathrm{2}} \\ $$$${I}_{\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\pi}\: \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}{U}_{{n}} =\frac{{I}_{\mathrm{1}} ^{\mathrm{2}} }{{I}_{\mathrm{2}} }=\frac{\frac{\pi}{\mathrm{4}}}{\frac{\mathrm{1}}{\mathrm{2}}×\sqrt{\frac{\pi}{{n}}}}=\frac{\pi×\mathrm{2}×\sqrt{{n}}}{\mathrm{4}×\sqrt{\pi}}=\frac{\sqrt{{n}\pi}}{\mathrm{2}} \\ $$$${sir}\:{pls}\:{che}\mathrm{4}{k}… \\ $$
