Menu Close

let-u-n-1-i-lt-j-n-1-ij-1-find-a-equivalent-of-u-n-2-calculate-lim-n-u-n-

Tinku Tara 0 Comments
Pin




Question Number 43003 by abdo.msup.com last updated on 06/Sep/18
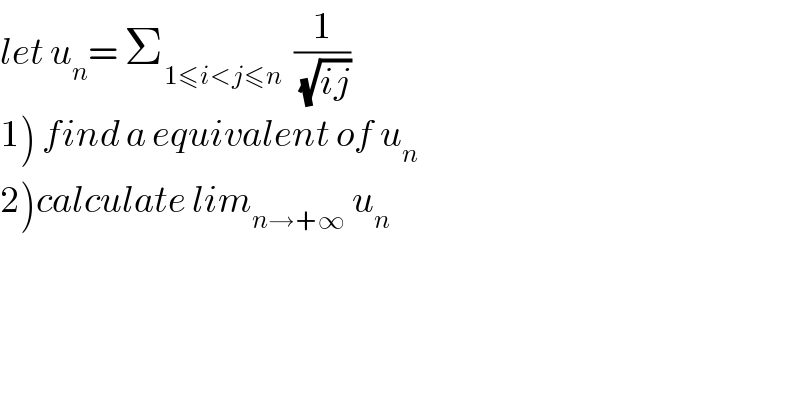
let u_n = Σ_(1≤i<j≤n) (1/( (√(ij)))) 1) find a equivalent of u_n 2)calculate lim_(n→+∞) u_n
$${let}\:{u}_{{n}} =\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\frac{\mathrm{1}}{\:\sqrt{{ij}}} \\ $$$$\left.\mathrm{1}\right)\:{find}\:{a}\:{equivalent}\:{of}\:{u}_{{n}} \\ $$$$\left.\mathrm{2}\right){calculate}\:{lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} \\ $$
Answered by maxmathsup by imad last updated on 07/Sep/18
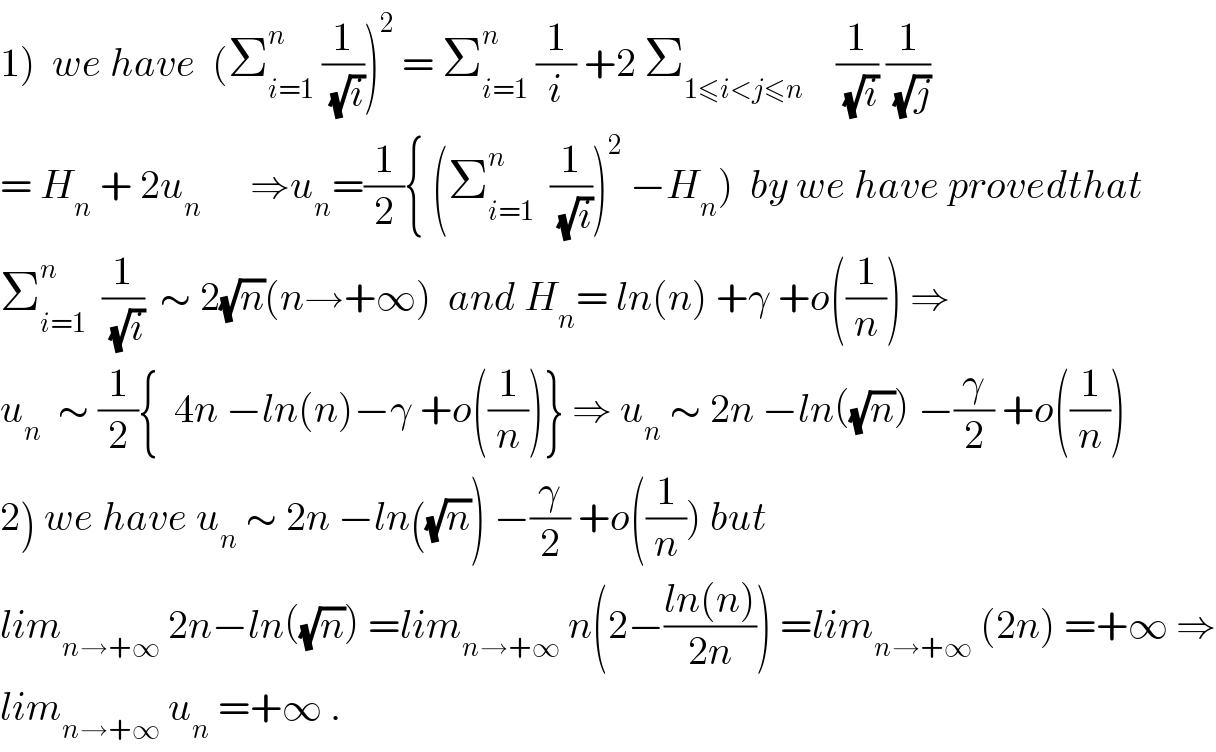
1) we have (Σ_(i=1) ^n (1/( (√i))))^2 = Σ_(i=1) ^n (1/i) +2 Σ_(1≤i<j≤n) (1/( (√i))) (1/( (√j))) = H_n + 2u_n ⇒u_n =(1/2){ (Σ_(i=1) ^n (1/( (√i))))^2 −H_n ) by we have provedthat Σ_(i=1) ^n (1/( (√i))) ∼ 2(√n)(n→+∞) and H_n = ln(n) +γ +o((1/n)) ⇒ u_n ∼ (1/2){ 4n −ln(n)−γ +o((1/n))} ⇒ u_n ∼ 2n −ln((√n)) −(γ/2) +o((1/n)) 2) we have u_n ∼ 2n −ln((√n)) −(γ/2) +o((1/n)) but lim_(n→+∞) 2n−ln((√n)) =lim_(n→+∞) n(2−((ln(n))/(2n))) =lim_(n→+∞) (2n) =+∞ ⇒ lim_(n→+∞) u_n =+∞ .
$$\left.\mathrm{1}\right)\:\:{we}\:{have}\:\:\left(\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{\:\sqrt{{i}}}\right)^{\mathrm{2}} \:=\:\sum_{{i}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{i}}\:+\mathrm{2}\:\sum_{\mathrm{1}\leqslant{i}<{j}\leqslant{n}} \:\:\:\:\frac{\mathrm{1}}{\:\sqrt{{i}}}\:\frac{\mathrm{1}}{\:\sqrt{{j}}} \\ $$$$=\:{H}_{{n}} \:+\:\mathrm{2}{u}_{{n}} \:\:\:\:\:\:\Rightarrow{u}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\left(\sum_{{i}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\:\sqrt{{i}}}\right)^{\mathrm{2}} \:−{H}_{{n}} \right)\:\:{by}\:{we}\:{have}\:{provedthat} \\ $$$$\sum_{{i}=\mathrm{1}} ^{{n}} \:\:\frac{\mathrm{1}}{\:\sqrt{{i}}}\:\:\sim\:\mathrm{2}\sqrt{{n}}\left({n}\rightarrow+\infty\right)\:\:{and}\:{H}_{{n}} =\:{ln}\left({n}\right)\:+\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\:\Rightarrow \\ $$$${u}_{{n}} \:\:\sim\:\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\:\mathrm{4}{n}\:−{ln}\left({n}\right)−\gamma\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\right\}\:\Rightarrow\:{u}_{{n}} \:\sim\:\mathrm{2}{n}\:−{ln}\left(\sqrt{{n}}\right)\:−\frac{\gamma}{\mathrm{2}}\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\: \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{u}_{{n}} \:\sim\:\mathrm{2}{n}\:−{ln}\left(\sqrt{{n}}\right)\:−\frac{\gamma}{\mathrm{2}}\:+{o}\left(\frac{\mathrm{1}}{{n}}\right)\:{but}\: \\ $$$${lim}_{{n}\rightarrow+\infty} \:\mathrm{2}{n}−{ln}\left(\sqrt{{n}}\right)\:={lim}_{{n}\rightarrow+\infty} \:{n}\left(\mathrm{2}−\frac{{ln}\left({n}\right)}{\mathrm{2}{n}}\right)\:={lim}_{{n}\rightarrow+\infty} \:\left(\mathrm{2}{n}\right)\:=+\infty\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{u}_{{n}} \:=+\infty\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *