Menu Close

let-u-n-1-n-2-n-3n-1-find-n-0-49-u-n-

Tinku Tara 0 Comments
Pin




Question Number 49937 by turbo msup by abdo last updated on 12/Dec/18
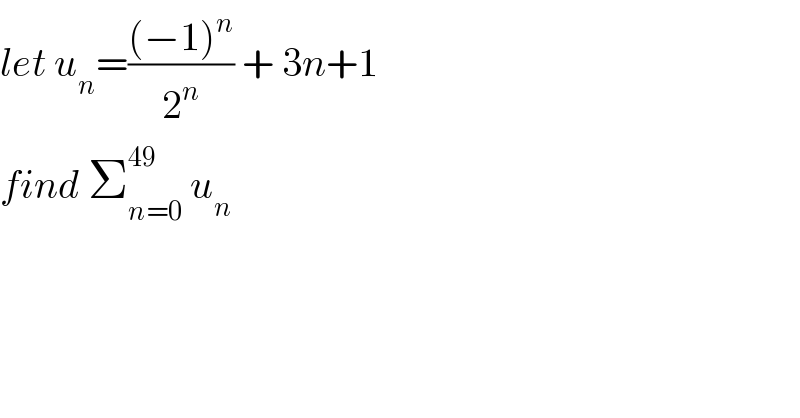
let u_n =(((−1)^n )/2^n ) + 3n+1 find Σ_(n=0) ^(49) u_n
$${let}\:{u}_{{n}} =\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\:+\:\mathrm{3}{n}+\mathrm{1} \\ $$$${find}\:\sum_{{n}=\mathrm{0}} ^{\mathrm{49}} \:{u}_{{n}} \\ $$
Commented by Abdo msup. last updated on 13/Dec/18
we have u_n =v_n +w_n with v_n =(−(1/2))^n geometric with q=−(1/2) and w_n =3n+1 srithmetic with r =3 Σ_(n=0) ^(49) u_n =Σ_(n=0) ^(49) u_n +Σ_(n=0) ^(49) w_n =u_0 ((1−q^(50) )/(1−q)) +((50)/2)(w_0 +w_n ) =((1−(−(1/2))^(50) )/(1+(1/2))) +25(1+3n+1) =(2/3)(1−(1/2^(50) )) +25(3n+2) .
$${we}\:{have}\:{u}_{{n}} ={v}_{{n}} \:+{w}_{{n}} \:\:{with}\:{v}_{{n}} =\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \:{geometric}\:{with}\:{q}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${and}\:{w}_{{n}} =\mathrm{3}{n}+\mathrm{1}\:{srithmetic}\:{with}\:{r}\:=\mathrm{3}\: \\ $$$$\sum_{{n}=\mathrm{0}} ^{\mathrm{49}} {u}_{{n}} =\sum_{{n}=\mathrm{0}} ^{\mathrm{49}} \:{u}_{{n}} \:+\sum_{{n}=\mathrm{0}} ^{\mathrm{49}} \:{w}_{{n}} \\ $$$$={u}_{\mathrm{0}} \:\frac{\mathrm{1}−{q}^{\mathrm{50}} }{\mathrm{1}−{q}}\:\:+\frac{\mathrm{50}}{\mathrm{2}}\left({w}_{\mathrm{0}} \:+{w}_{{n}} \right) \\ $$$$=\frac{\mathrm{1}−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{50}} }{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}}}\:+\mathrm{25}\left(\mathrm{1}+\mathrm{3}{n}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{50}} }\right)\:+\mathrm{25}\left(\mathrm{3}{n}+\mathrm{2}\right)\:. \\ $$
Commented by Abdo msup. last updated on 13/Dec/18
n=49 ⇒Σ_(n=0) ^(49) u_n =(2/3)(1−(1/2^(50) ))+25(3.49 +2) =(2/3)(1−(1/2^(50) )) +25.147 +2 =....
$${n}=\mathrm{49}\:\Rightarrow\sum_{{n}=\mathrm{0}} ^{\mathrm{49}} \:{u}_{{n}} =\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{50}} }\right)+\mathrm{25}\left(\mathrm{3}.\mathrm{49}\:+\mathrm{2}\right) \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{50}} }\right)\:+\mathrm{25}.\mathrm{147}\:+\mathrm{2}\:=…. \\ $$
Answered by afachri last updated on 12/Dec/18
Σ_(n = 0) ^(49) (((−1)^n )/2^n ) + 3n + 1 = Σ_(n = 1) ^(50) (2^(−1) )^(n − 1) + 3(n − 1) + 1 = Σ_(n = 1) ^(50) [_ ^ (2)^(1−n) + 3n − 2 _^ ] = Σ_(n = 1) ^(50) ((2/2^n ) + 3n − 2) Split the eq in three terms : = Σ_(n = 1) ^(50) ((2/2^n )) + 3Σ_(n = 1) ^(50) (n) − Σ_(n = 1) ^(50) (2) note : (2/2^n ) is geometric series with r = −(1/2) so the sigma will be its sum. S_(50) = ((a(1 − r^n ))/(1 − r)) = (((1(1 − (− (1/2))^(50) ))/(1 − (−(1/2))))) + 3(((50(51))/2)) − 2(50) = (2/3)(((2^(50) − 1)/2^(50) )) + 3825 − 100 The result for ((2^(50) − 1)/2^(50) ) is ≈ 1 = ((2(1))/3) + 3725 = 3725(2/3) [ Done ]
$$\underset{{n}\:=\:\:\mathrm{0}} {\overset{\mathrm{49}} {\sum}}\frac{\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\:+\:\mathrm{3}{n}\:+\:\mathrm{1}\:\:\:\:\:=\:\:\:\:\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{50}} {\sum}}\:\left(\mathrm{2}^{−\mathrm{1}} \right)^{{n}\:−\:\mathrm{1}} +\:\mathrm{3}\left({n}\:−\:\mathrm{1}\right)\:+\:\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\:\:\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{50}} {\sum}}\left[_{} ^{} \left(\mathrm{2}\right)^{\mathrm{1}−{n}} \:+\:\mathrm{3}{n}\:−\:\mathrm{2}\:_{} ^{} \right] \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\:\:\:\:\:\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{50}} {\sum}}\:\left(\frac{\mathrm{2}}{\mathrm{2}^{{n}} }\:\:+\:\mathrm{3}{n}\:−\:\mathrm{2}\right) \\ $$$$\mathrm{Split}\:\mathrm{the}\:\mathrm{eq}\:\mathrm{in}\:\mathrm{three}\:\mathrm{terms}\:: \\ $$$$\:\:=\:\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{50}} {\sum}}\:\left(\frac{\mathrm{2}}{\mathrm{2}^{{n}} }\right)\:\:\:\:+\:\:\:\mathrm{3}\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{50}} {\sum}}\:\left({n}\right)\:\:\:−\:\:\:\underset{{n}\:=\:\mathrm{1}} {\overset{\mathrm{50}} {\sum}}\left(\mathrm{2}\right)\: \\ $$$$\boldsymbol{\mathrm{note}}\::\:\frac{\mathrm{2}}{\mathrm{2}^{{n}} }\:\boldsymbol{\mathrm{is}}\:\boldsymbol{\mathrm{geometric}}\:\boldsymbol{\mathrm{series}}\:\boldsymbol{\mathrm{with}}\:\boldsymbol{{r}}\:=\:−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{sigma}}\:\boldsymbol{\mathrm{will}}\:\boldsymbol{\mathrm{be}}\:\boldsymbol{\mathrm{its}}\:\boldsymbol{\mathrm{sum}}.\:{S}_{\mathrm{50}} \:=\:\frac{{a}\left(\mathrm{1}\:−\:{r}^{{n}} \right)}{\mathrm{1}\:−\:{r}} \\ $$$$\:\:=\:\:\left(\frac{\mathrm{1}\left(\mathrm{1}\:−\:\left(−\:\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{50}} \right)}{\mathrm{1}\:−\:\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)}\right)\:\:\:\:+\:\:\:\:\mathrm{3}\left(\frac{\mathrm{50}\left(\mathrm{51}\right)}{\mathrm{2}}\right)\:\:\:\:−\:\:\:\mathrm{2}\left(\mathrm{50}\right) \\ $$$$\:\:=\:\:\:\frac{\mathrm{2}}{\mathrm{3}}\left(\frac{\mathrm{2}^{\mathrm{50}} −\:\mathrm{1}}{\mathrm{2}^{\mathrm{50}} }\right)\:\:\:\:\:+\:\:\:\:\mathrm{3825}\:\:\:−\:\:\:\mathrm{100} \\ $$$$\mathrm{The}\:\mathrm{result}\:\mathrm{for}\:\frac{\mathrm{2}^{\mathrm{50}} −\:\mathrm{1}}{\mathrm{2}^{\mathrm{50}} }\:\:\mathrm{is}\:\:\approx\:\mathrm{1}\:\:\: \\ $$$$\:\:\:=\:\:\frac{\mathrm{2}\left(\mathrm{1}\right)}{\mathrm{3}}\:\:\:+\:\:\:\mathrm{3725} \\ $$$$\:\:\:=\:\:\mathrm{3725}\frac{\mathrm{2}}{\mathrm{3}}\:\:\:\:\:\left[\:\:\mathrm{Done}\:\:\right] \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\: \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *