Menu Close

let-U-n-be-a-sequence-definied-by-U-0-1-U-n-1-3U-n-2-U-n-2-show-that-0-lt-U-n-lt-2-

Tinku Tara 0 Comments
Pin




Question Number 100640 by pticantor last updated on 27/Jun/20
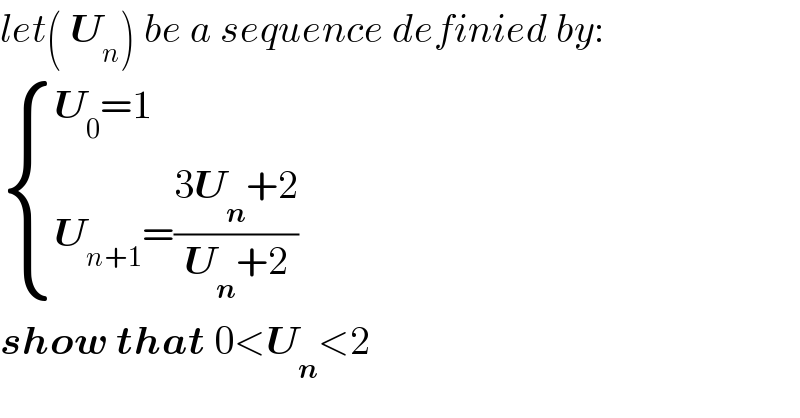
let( U_n ) be a sequence definied by: { ((U_0 =1)),((U_(n+1) =((3U_n +2)/(U_n +2)))) :} show that 0<U_n <2
$${let}\left(\:\boldsymbol{{U}}_{{n}} \right)\:{be}\:{a}\:{sequence}\:{definied}\:{by}: \\ $$$$\begin{cases}{\boldsymbol{{U}}_{\mathrm{0}} =\mathrm{1}}\\{\boldsymbol{{U}}_{{n}+\mathrm{1}} =\frac{\mathrm{3}\boldsymbol{{U}}_{\boldsymbol{{n}}} +\mathrm{2}}{\boldsymbol{{U}}_{\boldsymbol{{n}}} +\mathrm{2}}}\end{cases} \\ $$$$\boldsymbol{{show}}\:\boldsymbol{{that}}\:\mathrm{0}<\boldsymbol{{U}}_{\boldsymbol{{n}}} <\mathrm{2} \\ $$
Answered by maths mind last updated on 27/Jun/20
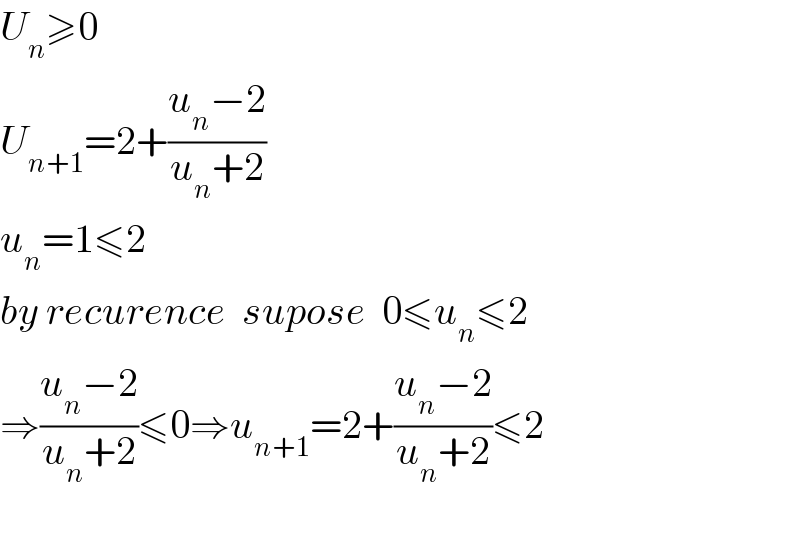
U_n ≥0 U_(n+1) =2+((u_n −2)/(u_n +2)) u_n =1≤2 by recurence supose 0≤u_n ≤2 ⇒((u_n −2)/(u_n +2))≤0⇒u_(n+1) =2+((u_n −2)/(u_n +2))≤2
$${U}_{{n}} \geqslant\mathrm{0} \\ $$$${U}_{{n}+\mathrm{1}} =\mathrm{2}+\frac{{u}_{{n}} −\mathrm{2}}{{u}_{{n}} +\mathrm{2}}\:\: \\ $$$${u}_{{n}} =\mathrm{1}\leqslant\mathrm{2}\:\: \\ $$$${by}\:{recurence}\:\:{supose}\:\:\mathrm{0}\leqslant{u}_{{n}} \leqslant\mathrm{2} \\ $$$$\Rightarrow\frac{{u}_{{n}} −\mathrm{2}}{{u}_{{n}} +\mathrm{2}}\leqslant\mathrm{0}\Rightarrow{u}_{{n}+\mathrm{1}} =\mathrm{2}+\frac{{u}_{{n}} −\mathrm{2}}{{u}_{{n}} +\mathrm{2}}\leqslant\mathrm{2} \\ $$$$ \\ $$
Commented by pticantor last updated on 28/Jun/20
thank you sir
$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}} \\ $$
Answered by 1549442205 last updated on 28/Jun/20
using induction method: +for n=0,u_0 =1∈(0;2)⇒state is true +suppose that the state is true for n=k which means that u_k =((3u_(k−1) +2)/(u_(k−1) +2))∈(0;2) +Consider u_(k+1) =((3u_k +2)/(u_k +2)).Clearly,u_(k+1) >0 u_(k+1) <2⇔((3u_k +2)/(u_k +2))<2⇔3u_k +2<2(u_k +2) ⇔u_k <2 .But this inequality is true by induction hypothesis ,so the inequality u_(k+1) <2 is true which show that the state is also true for n=k+1. Hence,by induction principle it is true for ∀n∈N(q.e.d) Furthermore,we can prove above sequence increasing and Lim_(n→∞) U_n =2
$$\mathrm{using}\:\mathrm{induction}\:\mathrm{method}: \\ $$$$+\mathrm{for}\:\mathrm{n}=\mathrm{0},\mathrm{u}_{\mathrm{0}} =\mathrm{1}\in\left(\mathrm{0};\mathrm{2}\right)\Rightarrow\mathrm{state}\:\mathrm{is}\:\mathrm{true} \\ $$$$+\mathrm{suppose}\:\mathrm{that}\:\mathrm{the}\:\mathrm{state}\:\mathrm{is}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{k} \\ $$$$\mathrm{which}\:\mathrm{means}\:\mathrm{that}\:\mathrm{u}_{\mathrm{k}} =\frac{\mathrm{3u}_{\mathrm{k}−\mathrm{1}} +\mathrm{2}}{\mathrm{u}_{\mathrm{k}−\mathrm{1}} +\mathrm{2}}\in\left(\mathrm{0};\mathrm{2}\right) \\ $$$$+\mathrm{Consider}\:\mathrm{u}_{\mathrm{k}+\mathrm{1}} =\frac{\mathrm{3u}_{\mathrm{k}} +\mathrm{2}}{\mathrm{u}_{\mathrm{k}} +\mathrm{2}}.\mathrm{Clearly},\mathrm{u}_{\mathrm{k}+\mathrm{1}} >\mathrm{0} \\ $$$$\mathrm{u}_{\mathrm{k}+\mathrm{1}} <\mathrm{2}\Leftrightarrow\frac{\mathrm{3u}_{\mathrm{k}} +\mathrm{2}}{\mathrm{u}_{\mathrm{k}} +\mathrm{2}}<\mathrm{2}\Leftrightarrow\mathrm{3u}_{\mathrm{k}} +\mathrm{2}<\mathrm{2}\left(\mathrm{u}_{\mathrm{k}} +\mathrm{2}\right) \\ $$$$\Leftrightarrow\mathrm{u}_{\mathrm{k}} <\mathrm{2}\:.\mathrm{But}\:\mathrm{this}\:\mathrm{inequality}\:\mathrm{is}\:\mathrm{true}\:\mathrm{by} \\ $$$$\mathrm{induction}\:\mathrm{hypothesis}\:,\mathrm{so}\:\mathrm{the}\:\mathrm{inequality}\: \\ $$$$\:\mathrm{u}_{\mathrm{k}+\mathrm{1}} <\mathrm{2}\:\mathrm{is}\:\mathrm{true}\:\mathrm{which}\:\mathrm{show}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{state}\:\mathrm{is}\:\mathrm{also}\:\mathrm{true}\:\mathrm{for}\:\mathrm{n}=\mathrm{k}+\mathrm{1}. \\ $$$$\mathrm{Hence},\mathrm{by}\:\mathrm{induction}\:\mathrm{principle}\:\mathrm{it}\:\mathrm{is}\:\mathrm{true} \\ $$$$\mathrm{for}\:\forall\mathrm{n}\in\mathbb{N}\left(\mathrm{q}.\mathrm{e}.\mathrm{d}\right) \\ $$$$\mathrm{Furthermore},\mathrm{we}\:\mathrm{can}\:\mathrm{prove}\:\mathrm{above}\:\mathrm{sequence} \\ $$$$\mathrm{increasing}\:\mathrm{and}\:\underset{\mathrm{n}\rightarrow\infty} {\mathrm{Lim}U}_{\mathrm{n}} =\mathrm{2} \\ $$$$ \\ $$
Commented by pticantor last updated on 28/Jun/20
thank you sir
$$\boldsymbol{{thank}}\:\boldsymbol{{you}}\:\boldsymbol{{sir}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *