Menu Close

let-u-n-e-1-1-n-n-n-2-2-n-2-1-find-lim-u-n-

Tinku Tara 0 Comments
Pin




Question Number 32364 by prof Abdo imad last updated on 23/Mar/18
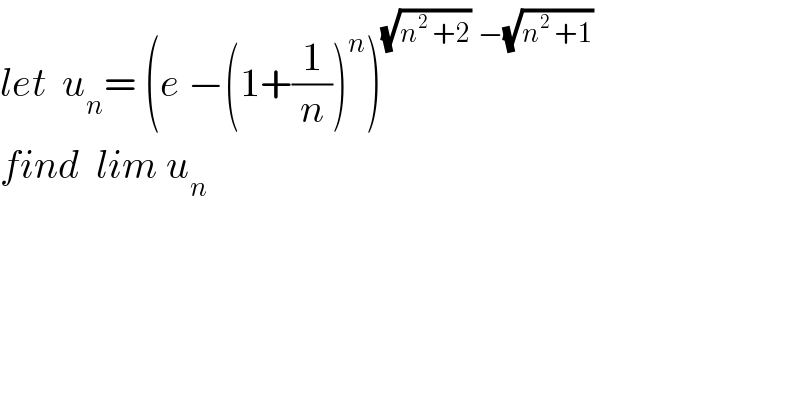
let u_n = (e −(1+(1/n))^n )^((√(n^2 +2)) −(√(n^2 +1))) find lim u_n
$${let}\:\:{u}_{{n}} =\:\left({e}\:−\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \right)^{\sqrt{{n}^{\mathrm{2}} \:+\mathrm{2}}\:\:−\sqrt{{n}^{\mathrm{2}} \:+\mathrm{1}}} \\ $$$${find}\:\:{lim}\:{u}_{{n}} \\ $$
Commented by prof Abdo imad last updated on 06/Apr/18
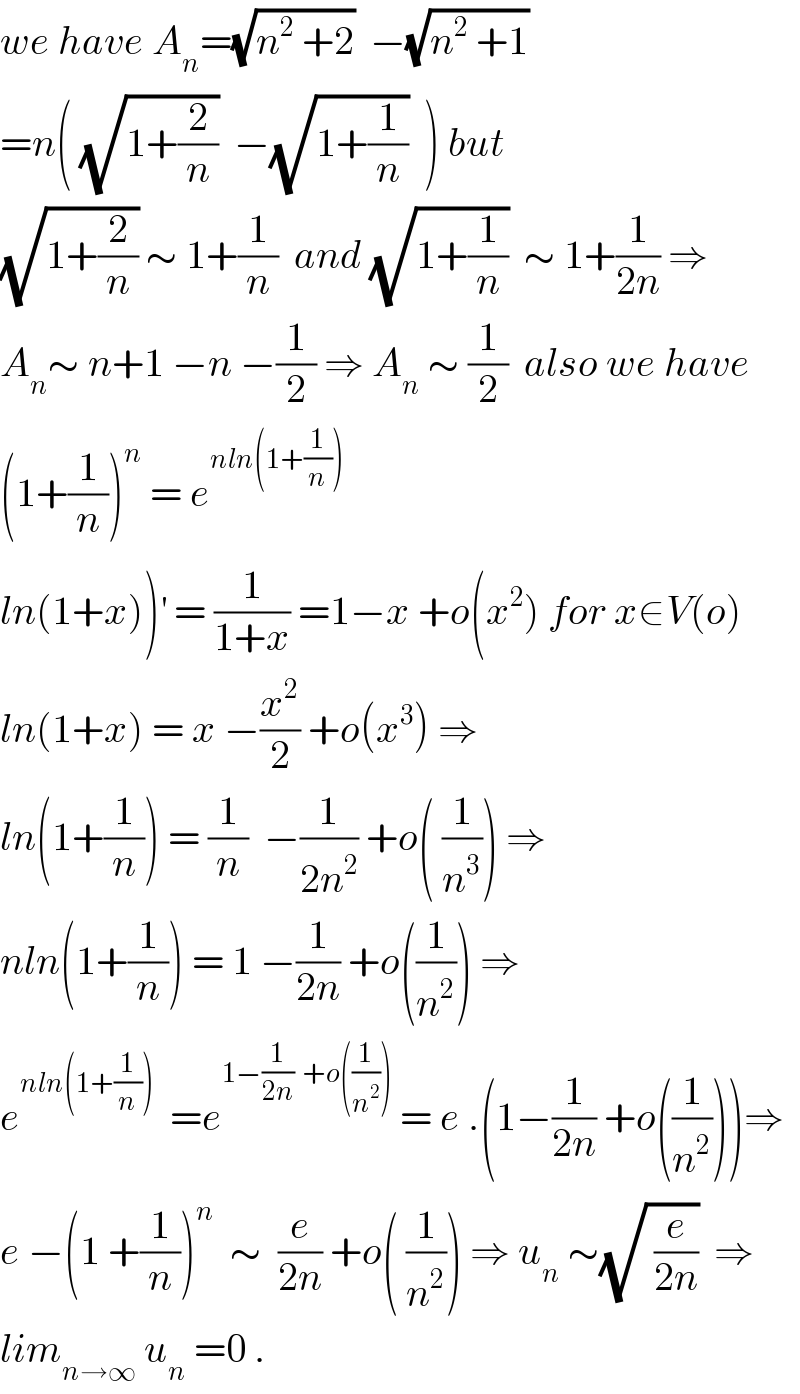
we have A_n =(√(n^2 +2)) −(√(n^2 +1)) =n( (√(1+(2/n))) −(√(1+(1/n))) ) but (√(1+(2/n))) ∼ 1+(1/n) and (√(1+(1/n))) ∼ 1+(1/(2n)) ⇒ A_n ∼ n+1 −n −(1/2) ⇒ A_n ∼ (1/2) also we have (1+(1/n))^n = e^(nln(1+(1/n))) ln(1+x))^′ = (1/(1+x)) =1−x +o(x^2 ) for x∈V(o) ln(1+x) = x −(x^2 /2) +o(x^3 ) ⇒ ln(1+(1/n)) = (1/n) −(1/(2n^2 )) +o( (1/n^3 )) ⇒ nln(1+(1/n)) = 1 −(1/(2n)) +o((1/n^2 )) ⇒ e^(nln(1+(1/n))) =e^(1−(1/(2n)) +o((1/n^2 ))) = e .(1−(1/(2n)) +o((1/n^2 )))⇒ e −(1 +(1/n))^n ∼ (e/(2n)) +o( (1/n^2 )) ⇒ u_n ∼(√( (e/(2n)))) ⇒ lim_(n→∞) u_n =0 .
$${we}\:{have}\:{A}_{{n}} =\sqrt{{n}^{\mathrm{2}} \:+\mathrm{2}}\:\:−\sqrt{{n}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$$={n}\left(\:\sqrt{\mathrm{1}+\frac{\mathrm{2}}{{n}}}\:\:−\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}}}\:\:\right)\:{but} \\ $$$$\sqrt{\mathrm{1}+\frac{\mathrm{2}}{{n}}}\:\sim\:\mathrm{1}+\frac{\mathrm{1}}{{n}}\:\:{and}\:\sqrt{\mathrm{1}+\frac{\mathrm{1}}{{n}}}\:\:\sim\:\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\:\Rightarrow \\ $$$${A}_{{n}} \sim\:{n}+\mathrm{1}\:−{n}\:−\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{A}_{{n}} \:\sim\:\frac{\mathrm{1}}{\mathrm{2}}\:\:{also}\:{we}\:{have} \\ $$$$\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{{n}} \:=\:{e}^{{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} \\ $$$$\left.{ln}\left(\mathrm{1}+{x}\right)\right)^{'} \:=\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:=\mathrm{1}−{x}\:+{o}\left({x}^{\mathrm{2}} \right)\:{for}\:{x}\in{V}\left({o}\right) \\ $$$${ln}\left(\mathrm{1}+{x}\right)\:=\:{x}\:−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:+{o}\left({x}^{\mathrm{3}} \right)\:\Rightarrow \\ $$$${ln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\:=\:\frac{\mathrm{1}}{{n}}\:\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }\:+{o}\left(\:\frac{\mathrm{1}}{{n}^{\mathrm{3}} }\right)\:\Rightarrow \\ $$$${nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)\:=\:\mathrm{1}\:−\frac{\mathrm{1}}{\mathrm{2}{n}}\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:\Rightarrow \\ $$$${e}^{{nln}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} \:\:={e}^{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\:\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)} \:=\:{e}\:.\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}{n}}\:+{o}\left(\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\right)\Rightarrow \\ $$$${e}\:−\left(\mathrm{1}\:+\frac{\mathrm{1}}{{n}}\right)^{{n}} \:\:\sim\:\:\frac{{e}}{\mathrm{2}{n}}\:+{o}\left(\:\frac{\mathrm{1}}{{n}^{\mathrm{2}} }\right)\:\Rightarrow\:{u}_{{n}} \:\sim\sqrt{\:\frac{{e}}{\mathrm{2}{n}}}\:\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow\infty} \:{u}_{{n}} \:=\mathrm{0}\:. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *