Question Number 41345 by maxmathsup by imad last updated on 05/Aug/18
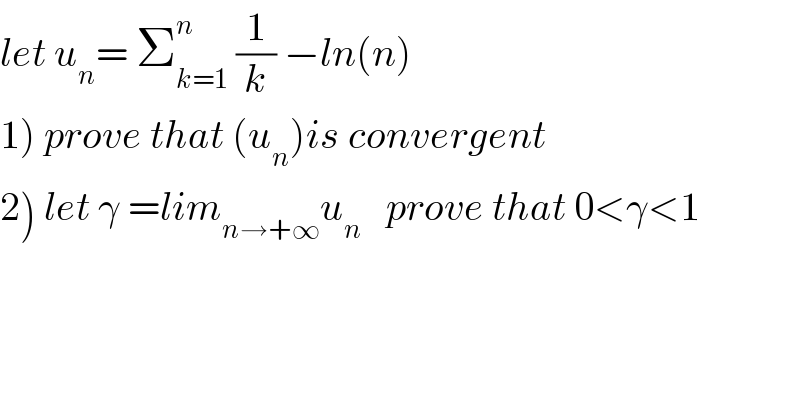
$${let}\:{u}_{{n}} =\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:−{ln}\left({n}\right) \\ $$$$\left.\mathrm{1}\right)\:{prove}\:{that}\:\left({u}_{{n}} \right){is}\:{convergent} \\ $$$$\left.\mathrm{2}\right)\:{let}\:\gamma\:={lim}_{{n}\rightarrow+\infty} {u}_{{n}} \:\:\:{prove}\:{that}\:\mathrm{0}<\gamma<\mathrm{1}\:\: \\ $$
Commented by alex041103 last updated on 06/Aug/18
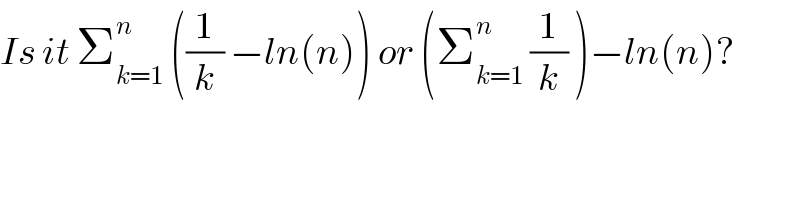
$${Is}\:{it}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\left(\frac{\mathrm{1}}{{k}}\:−{ln}\left({n}\right)\right)\:{or}\:\left(\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\:\right)−{ln}\left({n}\right)? \\ $$
Commented by math khazana by abdo last updated on 07/Aug/18

$$\left(\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{k}}\right)−{ln}\left({n}\right)\: \\ $$
