Question Number 30173 by abdo imad last updated on 18/Feb/18
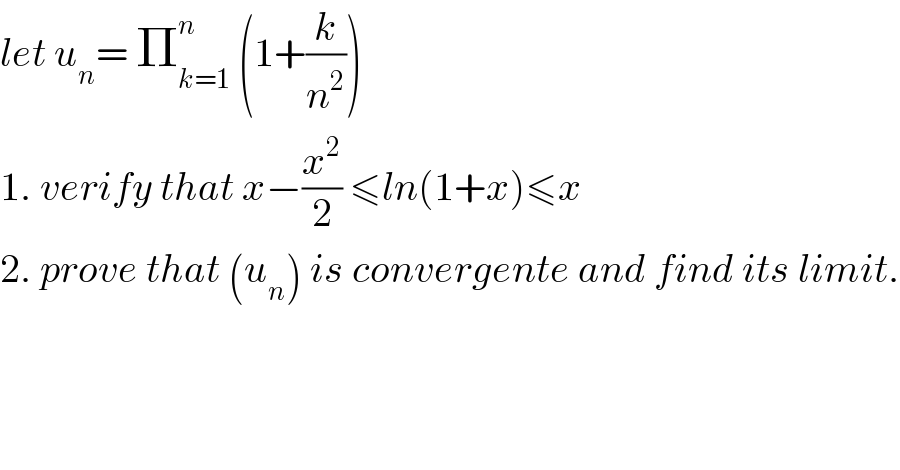
$${let}\:{u}_{{n}} =\:\prod_{{k}=\mathrm{1}} ^{{n}} \:\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right) \\ $$$$\mathrm{1}.\:{verify}\:{that}\:{x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\leqslant{ln}\left(\mathrm{1}+{x}\right)\leqslant{x} \\ $$$$\mathrm{2}.\:{prove}\:{that}\:\left({u}_{{n}} \right)\:{is}\:{convergente}\:{and}\:{find}\:{its}\:{limit}. \\ $$
Commented by abdo imad last updated on 21/Feb/18
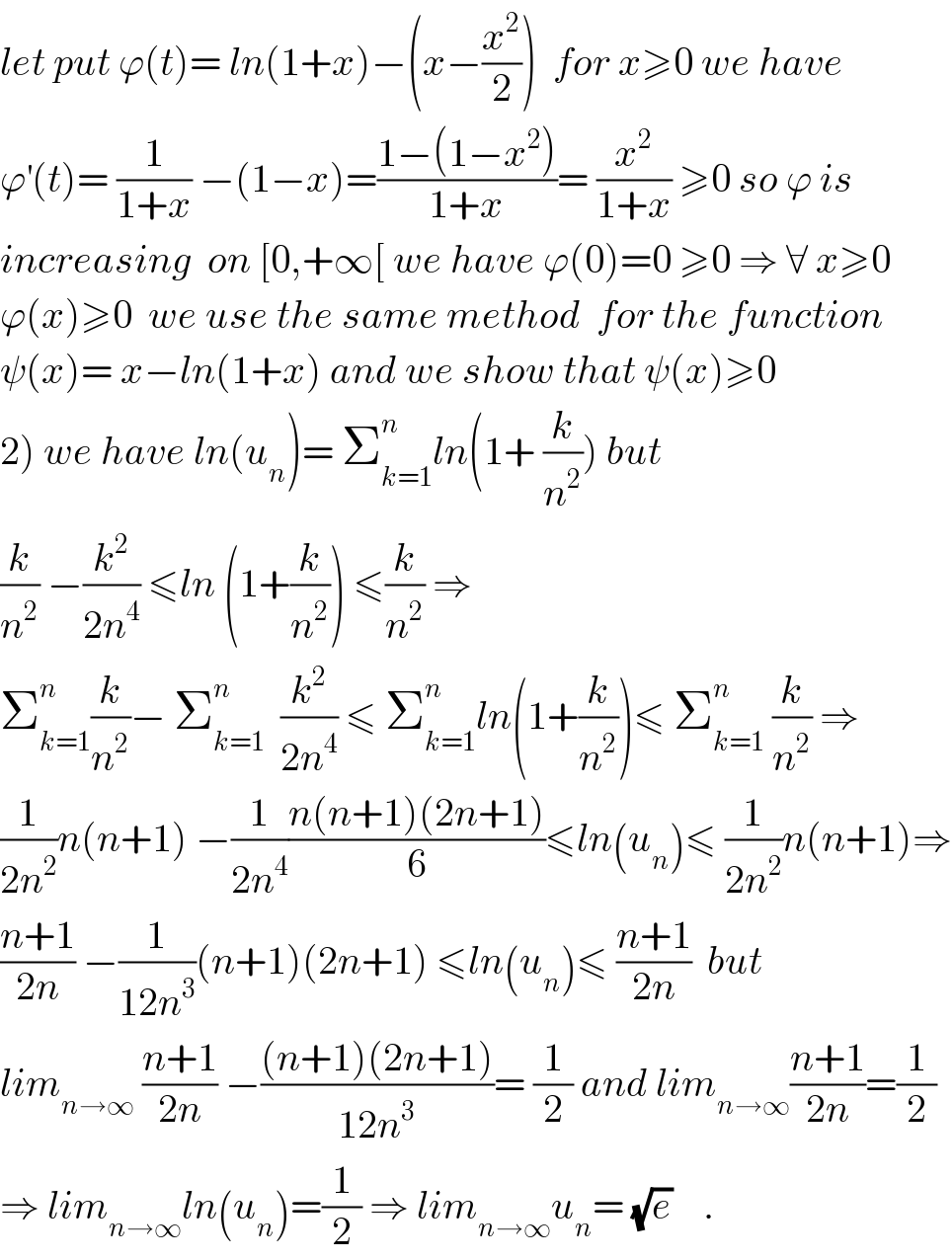
$${let}\:{put}\:\varphi\left({t}\right)=\:{ln}\left(\mathrm{1}+{x}\right)−\left({x}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}\right)\:\:{for}\:{x}\geqslant\mathrm{0}\:{we}\:{have} \\ $$$$\varphi^{'} \left({t}\right)=\:\frac{\mathrm{1}}{\mathrm{1}+{x}}\:−\left(\mathrm{1}−{x}\right)=\frac{\mathrm{1}−\left(\mathrm{1}−{x}^{\mathrm{2}} \right)}{\mathrm{1}+{x}}=\:\frac{{x}^{\mathrm{2}} }{\mathrm{1}+{x}}\:\geqslant\mathrm{0}\:{so}\:\varphi\:{is} \\ $$$${increasing}\:\:{on}\:\left[\mathrm{0},+\infty\left[\:{we}\:{have}\:\varphi\left(\mathrm{0}\right)=\mathrm{0}\:\geqslant\mathrm{0}\:\Rightarrow\:\forall\:{x}\geqslant\mathrm{0}\right.\right. \\ $$$$\varphi\left({x}\right)\geqslant\mathrm{0}\:\:{we}\:{use}\:{the}\:{same}\:{method}\:\:{for}\:{the}\:{function} \\ $$$$\psi\left({x}\right)=\:{x}−{ln}\left(\mathrm{1}+{x}\right)\:{and}\:{we}\:{show}\:{that}\:\psi\left({x}\right)\geqslant\mathrm{0} \\ $$$$\left.\mathrm{2}\right)\:{we}\:{have}\:{ln}\left({u}_{{n}} \right)=\:\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\:\frac{{k}}{{n}^{\mathrm{2}} }\right)\:{but}\: \\ $$$$\frac{{k}}{{n}^{\mathrm{2}} }\:−\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\:\leqslant{ln}\:\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\:\leqslant\frac{{k}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\sum_{{k}=\mathrm{1}} ^{{n}} \frac{{k}}{{n}^{\mathrm{2}} }−\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\:\frac{{k}^{\mathrm{2}} }{\mathrm{2}{n}^{\mathrm{4}} }\:\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} {ln}\left(\mathrm{1}+\frac{{k}}{{n}^{\mathrm{2}} }\right)\leqslant\:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{{k}}{{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }{n}\left({n}+\mathrm{1}\right)\:−\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{4}} }\frac{{n}\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{6}}\leqslant{ln}\left({u}_{{n}} \right)\leqslant\:\frac{\mathrm{1}}{\mathrm{2}{n}^{\mathrm{2}} }{n}\left({n}+\mathrm{1}\right)\Rightarrow \\ $$$$\frac{{n}+\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\mathrm{1}}{\mathrm{12}{n}^{\mathrm{3}} }\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)\:\leqslant{ln}\left({u}_{{n}} \right)\leqslant\:\frac{{n}+\mathrm{1}}{\mathrm{2}{n}}\:\:{but} \\ $$$${lim}_{{n}\rightarrow\infty} \:\frac{{n}+\mathrm{1}}{\mathrm{2}{n}}\:−\frac{\left({n}+\mathrm{1}\right)\left(\mathrm{2}{n}+\mathrm{1}\right)}{\mathrm{12}{n}^{\mathrm{3}} }=\:\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{lim}_{{n}\rightarrow\infty} \frac{{n}+\mathrm{1}}{\mathrm{2}{n}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\Rightarrow\:{lim}_{{n}\rightarrow\infty} {ln}\left({u}_{{n}} \right)=\frac{\mathrm{1}}{\mathrm{2}}\:\Rightarrow\:{lim}_{{n}\rightarrow\infty} {u}_{{n}} =\:\sqrt{{e}}\:\:\:\:. \\ $$
