let-u-n-k-1-n-1-n-k-n-k-1-find-a-equivalent-of-u-n-n-

Question Number 40898 by abdo.msup.com last updated on 28/Jul/18

l e t u_{n} = \sum_{k = 1}^{n - 1} \frac{n - k}{n - k + 1}

f i n d a e q u i v a l e n t o f u_{n} (n \to + \infty)

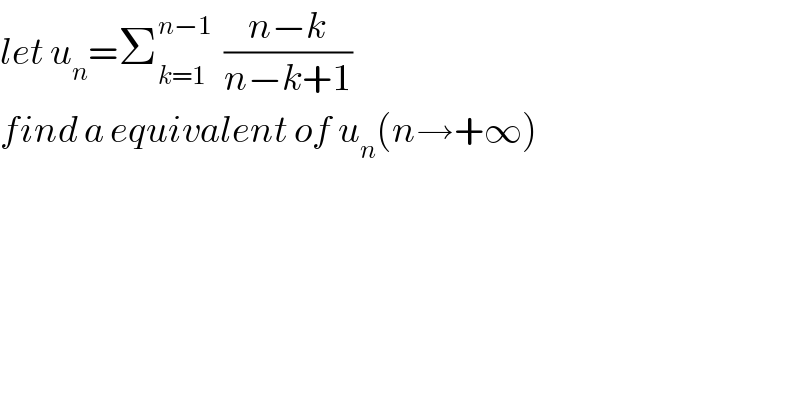
Commented by maxmathsup by imad last updated on 29/Jul/18

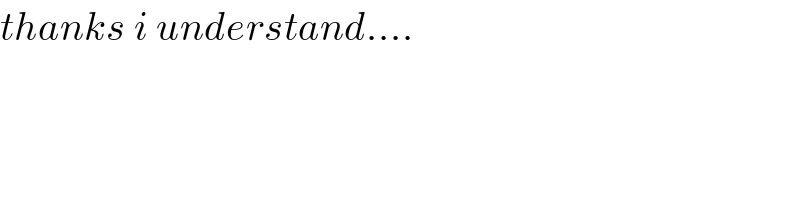
t h a n k s i u n d e r s t a n d \dots .

Answered by tanmay.chaudhury50@gmail.com last updated on 29/Jul/18

T_{k} = 1 - \frac{1}{n + 1 - k}

T_{1} = 1 - \frac{1}{n}

T_{2} = 1 - \frac{1}{n - 1}

\dots

\dots

T_{n - 1} = 1 - \frac{1}{2}

s o u_{n} = (n - 1) - {\frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n}} t o f i n d

u_{n} = (n - 1) - s

v a l u e o f u_{n} n \to \infty

1 > \frac{1}{2} > \frac{1}{n}

1 > \frac{1}{3} > \frac{1}{n}

1 > \frac{1}{4} > \frac{1}{n}

\dots . .

\dots \dots

s o a d d i n g n - 1 > s > \frac{n - 1}{n}

- (n - 1) < - s < - (\frac{n - 1}{n})

(n - 1) - (n - 1) < (n - 1) - s < (n - 1) - (\frac{n - 1}{n})

0 < u_{n} < n - 1 - 1 + \frac{1}{n}

0 < u_{n} < n + \frac{1}{n} - 2

0 < u_{n} < {(\sqrt{n} - \frac{1}{\sqrt{n_{}}})}^{2}

w h e n n \to \infty \infty > u_{n} > 0

p l s c h e c k \dots .

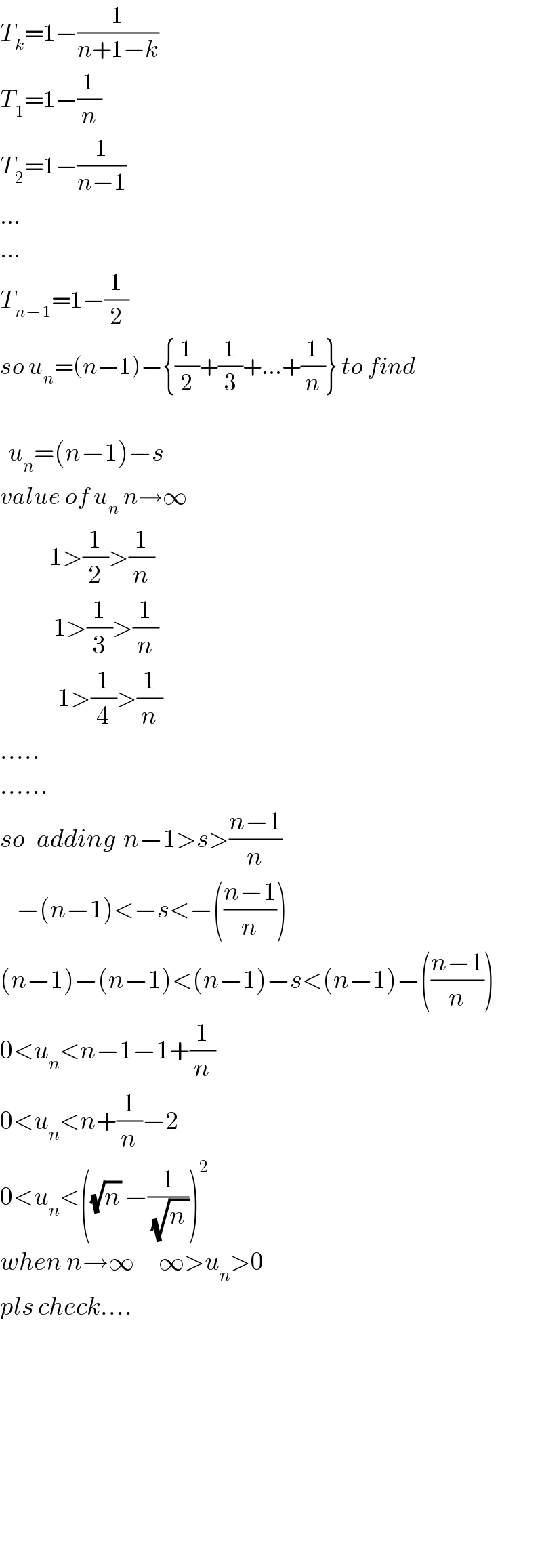
Answered by math khazana by abdo last updated on 29/Jul/18

w e h a v e u_{n} = \sum_{k = 1}^{n - 1} \frac{n - k + 1 - 1}{n - k + 1}

= \sum_{k = 1}^{n - 1} (1) - \sum_{k = 1}^{n - 1} \frac{1}{n - k + 1} b u t

\sum_{k = 1}^{n - 1} (1) = n - 1 a n d

\sum_{k = 1}^{n - 1} \frac{1}{n - k + 1} =_{n - k = i} \sum_{i = n - 1}^{1} \frac{1}{i + 1} = \sum_{i = 1}^{n - 1} \frac{1}{i + 1}

= \sum_{i = 2}^{n} \frac{1}{i} = H_{n} - 1 \Rightarrow

u_{n} = n - 1 - H_{n} + 1 = n - H_{n} b u t

H_{n} = l n (n) + γ + o (\frac{1}{n}) \Rightarrow u_{n} = n - l n (n) - γ + o (\frac{1}{n}) \Rightarrow

u_{n} \sim n - l n (n) (n \to + \infty)

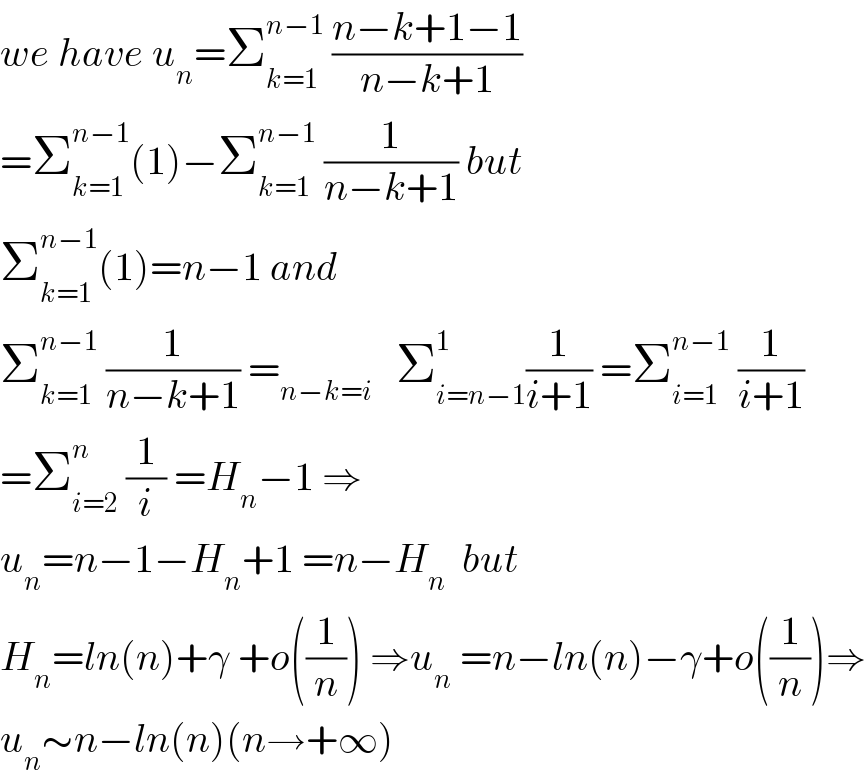
Commented by math khazana by abdo last updated on 29/Jul/18

H_{n} = \sum_{k = 1}^{n} \frac{1}{k}