Menu Close

let-u-n-ln-cos-2-n-calculate-n-0-u-n-

Tinku Tara 0 Comments
Pin




Question Number 52678 by maxmathsup by imad last updated on 11/Jan/19
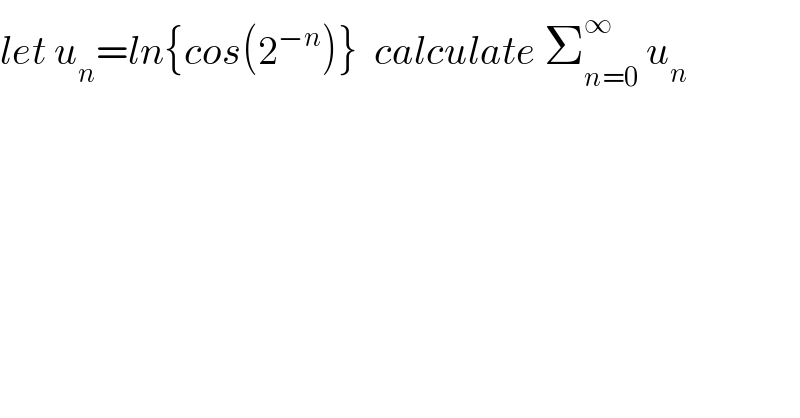
let u_n =ln{cos(2^(−n) )} calculate Σ_(n=0) ^∞ u_n
$${let}\:{u}_{{n}} ={ln}\left\{{cos}\left(\mathrm{2}^{−{n}} \right)\right\}\:\:{calculate}\:\sum_{{n}=\mathrm{0}} ^{\infty} \:{u}_{{n}} \\ $$
Commented by Abdo msup. last updated on 12/Jan/19
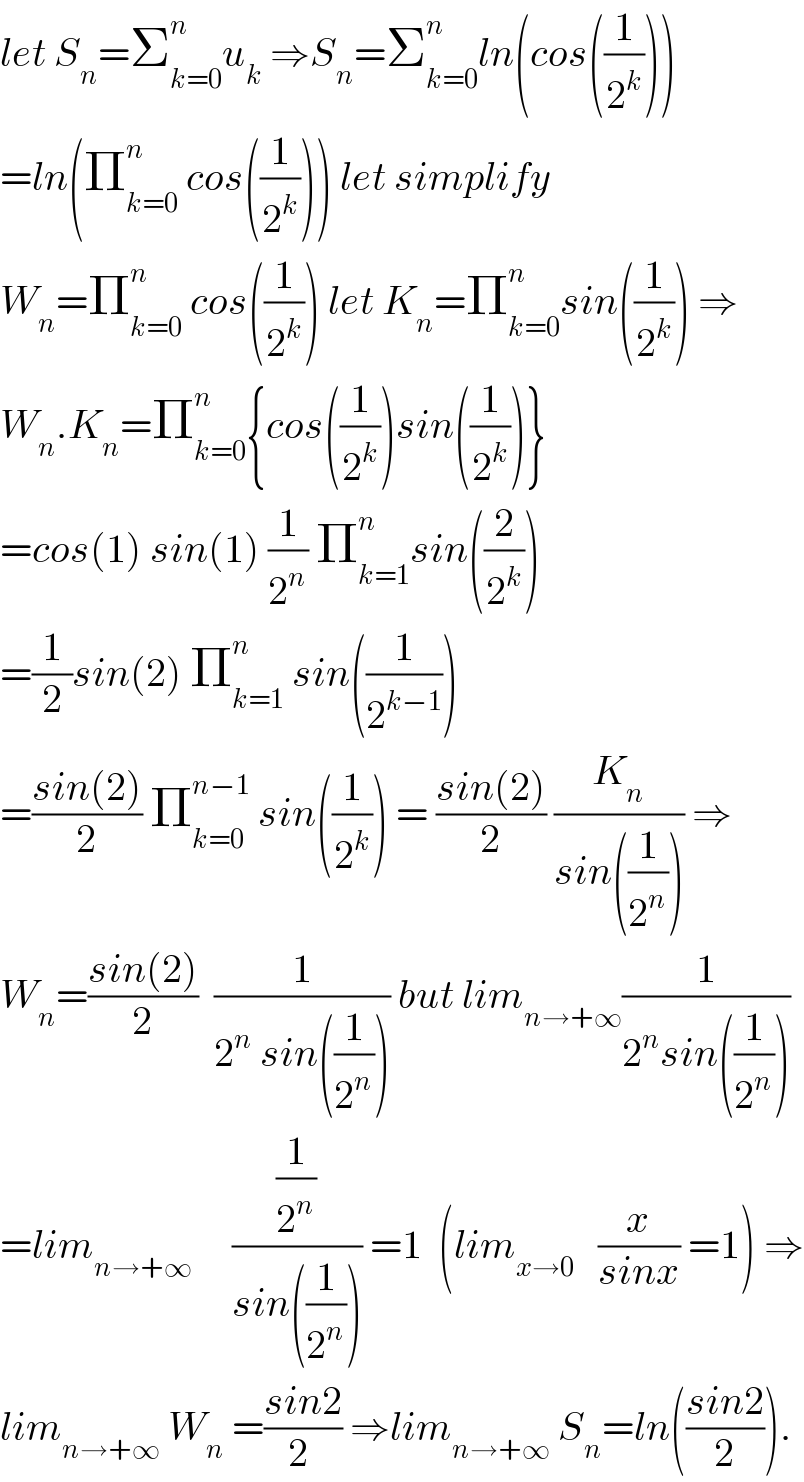
let S_n =Σ_(k=0) ^n u_k ⇒S_n =Σ_(k=0) ^n ln(cos((1/2^k ))) =ln(Π_(k=0) ^n cos((1/2^k ))) let simplify W_n =Π_(k=0) ^n cos((1/2^k )) let K_n =Π_(k=0) ^n sin((1/2^k )) ⇒ W_n .K_n =Π_(k=0) ^n {cos((1/2^k ))sin((1/2^k ))} =cos(1) sin(1) (1/2^n ) Π_(k=1) ^n sin((2/2^k )) =(1/2)sin(2) Π_(k=1) ^n sin((1/2^(k−1) )) =((sin(2))/2) Π_(k=0) ^(n−1) sin((1/2^k )) = ((sin(2))/2) (K_n /(sin((1/2^n )))) ⇒ W_n =((sin(2))/2) (1/(2^n sin((1/2^n )))) but lim_(n→+∞) (1/(2^n sin((1/2^n )))) =lim_(n→+∞) ((1/2^n )/(sin((1/2^n )))) =1 (lim_(x→0) (x/(sinx)) =1) ⇒ lim_(n→+∞) W_n =((sin2)/(2 )) ⇒lim_(n→+∞) S_n =ln(((sin2)/2)).
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} {u}_{{k}} \:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} {ln}\left({cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)\right) \\ $$$$={ln}\left(\prod_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)\right)\:{let}\:{simplify}\: \\ $$$${W}_{{n}} =\prod_{{k}=\mathrm{0}} ^{{n}} \:{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)\:{let}\:{K}_{{n}} =\prod_{{k}=\mathrm{0}} ^{{n}} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)\:\Rightarrow \\ $$$${W}_{{n}} .{K}_{{n}} =\prod_{{k}=\mathrm{0}} ^{{n}} \left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right){sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)\right\} \\ $$$$={cos}\left(\mathrm{1}\right)\:{sin}\left(\mathrm{1}\right)\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\:\prod_{{k}=\mathrm{1}} ^{{n}} {sin}\left(\frac{\mathrm{2}}{\mathrm{2}^{{k}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{sin}\left(\mathrm{2}\right)\:\prod_{{k}=\mathrm{1}} ^{{n}} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}−\mathrm{1}} }\right) \\ $$$$=\frac{{sin}\left(\mathrm{2}\right)}{\mathrm{2}}\:\prod_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{k}} }\right)\:=\:\frac{{sin}\left(\mathrm{2}\right)}{\mathrm{2}}\:\frac{{K}_{{n}} }{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)}\:\Rightarrow \\ $$$${W}_{{n}} =\frac{{sin}\left(\mathrm{2}\right)}{\mathrm{2}}\:\:\frac{\mathrm{1}}{\mathrm{2}^{{n}} \:{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)}\:{but}\:{lim}_{{n}\rightarrow+\infty} \frac{\mathrm{1}}{\mathrm{2}^{{n}} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)} \\ $$$$={lim}_{{n}\rightarrow+\infty} \:\:\:\:\:\frac{\frac{\mathrm{1}}{\mathrm{2}^{{n}} }}{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)}\:=\mathrm{1}\:\:\left({lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\frac{{x}}{{sinx}}\:=\mathrm{1}\right)\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{W}_{{n}} \:=\frac{{sin}\mathrm{2}}{\mathrm{2}\:}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} ={ln}\left(\frac{{sin}\mathrm{2}}{\mathrm{2}}\right). \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 12/Jan/19
u_0 +u_1 +u_2 +...+u_n +...∞ =ln{cos((1/2^0 ))}+ln{cos((1/2^1 ))}+ln{cos((1/2^2 ))}+..+ln{cos((1/2^(n−1) ))}+..∞ =ln{cos((1/2^0 ))cos((1/2^1 ))cos((1/2^2 ))..cos((1/2^(n−1) ))...∞}t now sin(2)=2sin1cos1 =2^2 sin((1/2))(cos((1/2))cos1 =2^3 sin((1/2^2 ))cos((1/2^2 ))cos((1/2))cos((1/2^0 )) thus required ans is ln{((sin2)/(2^n sin((1/2^(n−1) )))}when n→∞ lim_(n→0∞) ((sin((1/2^(n−1) )))/2^(n−1) )→1 so answer is ln(((sin2)/2)) another approach... formula sinθ=θcos((θ/2))cos((θ/2^2 ))cos((θ/2^3 ))...∞ here u_n =ln{cos((1/2^n ))} u_0 +u_1 +u_2 +...∞ ln{cos((1/2^0 ))}+ln{cos((1/2^1 ))}+ln{cos((1/2^2 ))}+...∞ =ln{cos((1/2^0 ))cos((1/2^1 ))cos((1/2^2 ))...∞} =ln{cos((1/2^0 ))×((sin1)/1)} [put θ=1] =ln{((2sin1cos1)/2)} =ln(((sin2)/2)) pls check....
$${u}_{\mathrm{0}} +{u}_{\mathrm{1}} +{u}_{\mathrm{2}} +…+{u}_{{n}} +…\infty \\ $$$$={ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }\right)\right\}+{ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }\right)\right\}+{ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\right\}+..+{ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)\right\}+..\infty \\ $$$$={ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)..{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)…\infty\right\}{t} \\ $$$${now} \\ $$$${sin}\left(\mathrm{2}\right)=\mathrm{2}{sin}\mathrm{1}{cos}\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{2}} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\left({cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){cos}\mathrm{1}\right. \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{2}^{\mathrm{3}} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}}\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }\right) \\ $$$${thus}\:{required}\:{ans}\:{is} \\ $$$${ln}\left\{\frac{{sin}\mathrm{2}}{\mathrm{2}^{{n}} {sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right.}\right\}{when}\:{n}\rightarrow\infty \\ $$$$\underset{{n}\rightarrow\mathrm{0}\infty} {\mathrm{lim}}\:\:\frac{{sin}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}−\mathrm{1}} }\right)}{\mathrm{2}^{{n}−\mathrm{1}} }\rightarrow\mathrm{1} \\ $$$${so}\:{answer}\:{is}\:{ln}\left(\frac{{sin}\mathrm{2}}{\mathrm{2}}\right) \\ $$$${another}\:{approach}… \\ $$$${formula} \\ $$$${sin}\theta=\theta{cos}\left(\frac{\theta}{\mathrm{2}}\right){cos}\left(\frac{\theta}{\mathrm{2}^{\mathrm{2}} }\right){cos}\left(\frac{\theta}{\mathrm{2}^{\mathrm{3}} }\right)…\infty \\ $$$${here}\:{u}_{{n}} ={ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{{n}} }\right)\right\} \\ $$$${u}_{\mathrm{0}} +{u}_{\mathrm{1}} +{u}_{\mathrm{2}} +…\infty \\ $$$${ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }\right)\right\}+{ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }\right)\right\}+{ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)\right\}+…\infty \\ $$$$={ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{1}} }\right){cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)…\infty\right\} \\ $$$$={ln}\left\{{cos}\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{0}} }\right)×\frac{{sin}\mathrm{1}}{\mathrm{1}}\right\}\:\:\:\left[{put}\:\theta=\mathrm{1}\right] \\ $$$$={ln}\left\{\frac{\mathrm{2}{sin}\mathrm{1}{cos}\mathrm{1}}{\mathrm{2}}\right\} \\ $$$$={ln}\left(\frac{{sin}\mathrm{2}}{\mathrm{2}}\right) \\ $$$${pls}\:{check}…. \\ $$
Commented by Abdo msup. last updated on 12/Jan/19
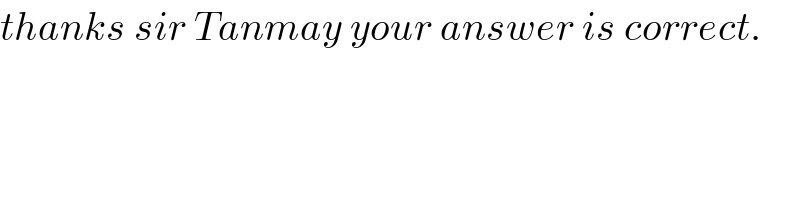
thanks sir Tanmay your answer is correct.
$${thanks}\:{sir}\:{Tanmay}\:{your}\:{answer}\:{is}\:{correct}. \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *