Question Number 57668 by maxmathsup by imad last updated on 09/Apr/19
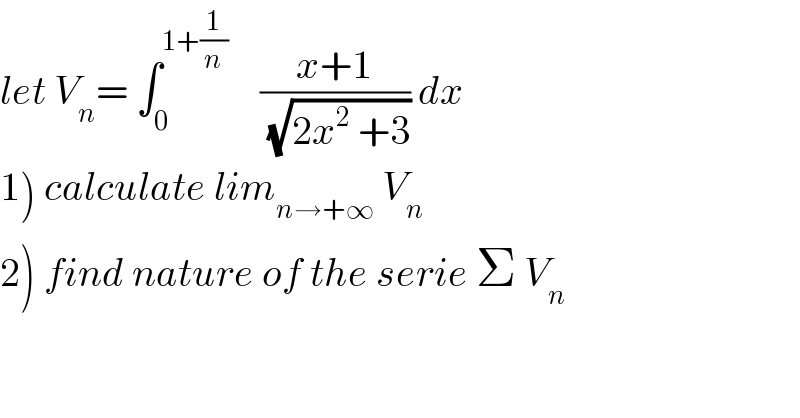
$${let}\:{V}_{{n}} =\:\int_{\mathrm{0}} ^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} \:\:\:\:\frac{{x}+\mathrm{1}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}}}\:{dx}\:\: \\ $$$$\left.\mathrm{1}\right)\:{calculate}\:{lim}_{{n}\rightarrow+\infty} \:{V}_{{n}} \\ $$$$\left.\mathrm{2}\right)\:{find}\:{nature}\:{of}\:{the}\:{serie}\:\Sigma\:{V}_{{n}} \\ $$
Commented by maxmathsup by imad last updated on 10/Apr/19
![1) we have V_n =∫_0 ^(1+(1/n)) (x/( (√(2x^2 +3))))dx +∫_0 ^(1+(1/n)) (dx/( (√(2x^2 +3)))) ∫_0 ^(1+(1/n)) (x/( (√(2x^2 +3)))) dx [(1/2)(√(2x^2 +3))]_0 ^(1+(1/n)) =(1/2){(√(2(1+(1/n))^2 +3))−(√3)} ∫_0 ^(1+(1/n)) (dx/( (√(2x^2 +3)))) =_((√2)x =(√3)u) ∫_0 ^(((√2)/( (√3)))(1+(1/n))) (1/( (√3)(√(1+u^2 )))) ((√3)/( (√2))) du =(1/( (√2))) ∫_0 ^(((√2)/( (√3)))(1+(1/n))) (du/( (√(1+u^2 )))) =[ln(u+(√(1+u^2 ))]_0 ^(((√2)/( (√3)))(1+(1/n))) =ln( (√(2/3))(1+(1/n))+(√(1+(2/3)(1+(1/n))^2 ))) ⇒ V_n =(1/2){ (√(2(1+(1/n))^2 +3))−(√3)}+ln{((√2)/( (√3)))(1+(1/n))+(√(1+(2/3)(1+(1/n))^2 ))} ⇒ lim_(n→+∞) V_n =(1/2){(√5)−(√3)} +ln{(((√2)+(√5))/( (√3)))} .](https://www.tinkutara.com/question/Q57682.png)
$$\left.\mathrm{1}\right)\:{we}\:{have}\:{V}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} \:\:\frac{{x}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}}}{dx}\:+\int_{\mathrm{0}} ^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} \:\:\frac{{x}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}}}\:{dx}\:\left[\frac{\mathrm{1}}{\mathrm{2}}\sqrt{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}}\right]_{\mathrm{0}} ^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} \:=\frac{\mathrm{1}}{\mathrm{2}}\left\{\sqrt{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} \:+\mathrm{3}}−\sqrt{\mathrm{3}}\right\} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} \:\:\frac{{dx}}{\:\sqrt{\mathrm{2}{x}^{\mathrm{2}} \:+\mathrm{3}}}\:=_{\sqrt{\mathrm{2}}{x}\:=\sqrt{\mathrm{3}}{u}} \:\:\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} \:\:\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }}\:\frac{\sqrt{\mathrm{3}}}{\:\sqrt{\mathrm{2}}}\:{du}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\:\int_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} \:\:\frac{{du}}{\:\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }} \\ $$$$=\left[{ln}\left({u}+\sqrt{\mathrm{1}+{u}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)} \:={ln}\left(\:\sqrt{\frac{\mathrm{2}}{\mathrm{3}}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)+\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} }\right)\:\Rightarrow\right. \\ $$$${V}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\sqrt{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} +\mathrm{3}}−\sqrt{\mathrm{3}}\right\}+{ln}\left\{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)+\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} }\right\}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} {V}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\sqrt{\mathrm{5}}−\sqrt{\mathrm{3}}\right\}\:+{ln}\left\{\frac{\sqrt{\mathrm{2}}+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}}\right\}\:. \\ $$
Commented by maxmathsup by imad last updated on 10/Apr/19
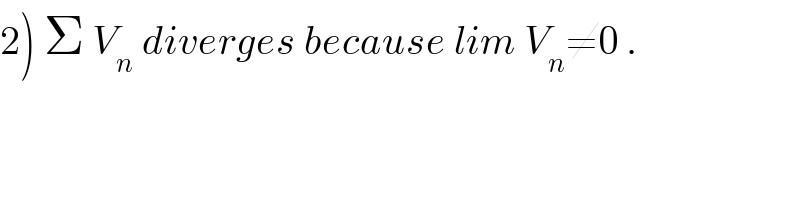
$$\left.\mathrm{2}\right)\:\Sigma\:{V}_{{n}} \:{diverges}\:{because}\:{lim}\:{V}_{{n}} \neq\mathrm{0}\:. \\ $$
Commented by Abdo msup. last updated on 10/Apr/19
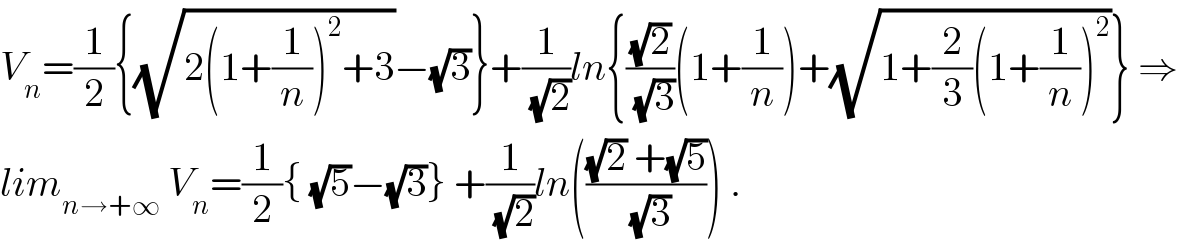
$${V}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\sqrt{\mathrm{2}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} +\mathrm{3}}−\sqrt{\mathrm{3}}\right\}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{ln}\left\{\frac{\sqrt{\mathrm{2}}}{\:\sqrt{\mathrm{3}}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)+\sqrt{\mathrm{1}+\frac{\mathrm{2}}{\mathrm{3}}\left(\mathrm{1}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} }\right\}\:\Rightarrow \\ $$$${lim}_{{n}\rightarrow+\infty} \:{V}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}\left\{\:\sqrt{\mathrm{5}}−\sqrt{\mathrm{3}}\right\}\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}{ln}\left(\frac{\sqrt{\mathrm{2}}\:+\sqrt{\mathrm{5}}}{\:\sqrt{\mathrm{3}}}\right)\:. \\ $$
