Question Number 173116 by ali009 last updated on 06/Jul/22
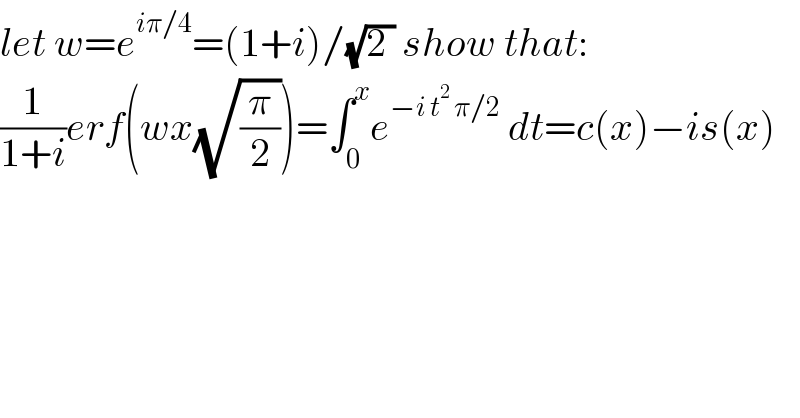
$${let}\:{w}={e}^{{i}\pi/\mathrm{4}} =\left(\mathrm{1}+{i}\right)/\sqrt{\mathrm{2}\:}\:{show}\:{that}: \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{i}}{erf}\left({wx}\sqrt{\frac{\pi}{\mathrm{2}}}\right)=\int_{\mathrm{0}} ^{{x}} {e}^{−{i}\:{t}^{\mathrm{2}} \:\pi/\mathrm{2}} \:{dt}={c}\left({x}\right)−{is}\left({x}\right) \\ $$
Commented by ali009 last updated on 06/Jul/22
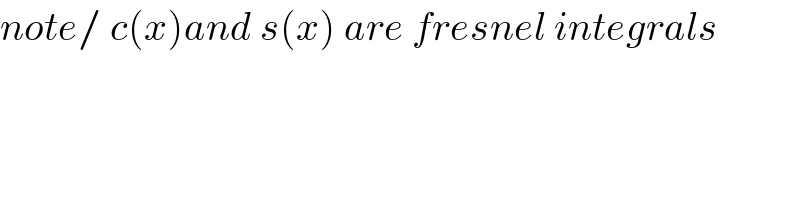
$${note}/\:{c}\left({x}\right){and}\:{s}\left({x}\right)\:{are}\:{fresnel}\:{integrals} \\ $$
