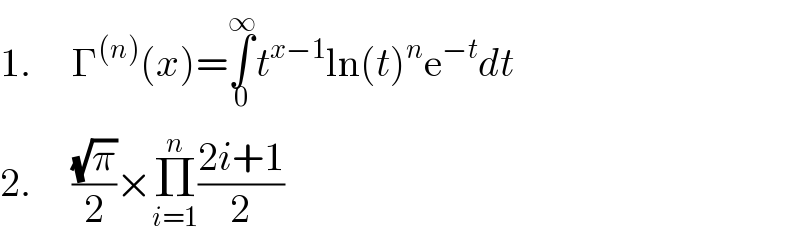Question Number 33915 by prof Abdo imad last updated on 27/Apr/18
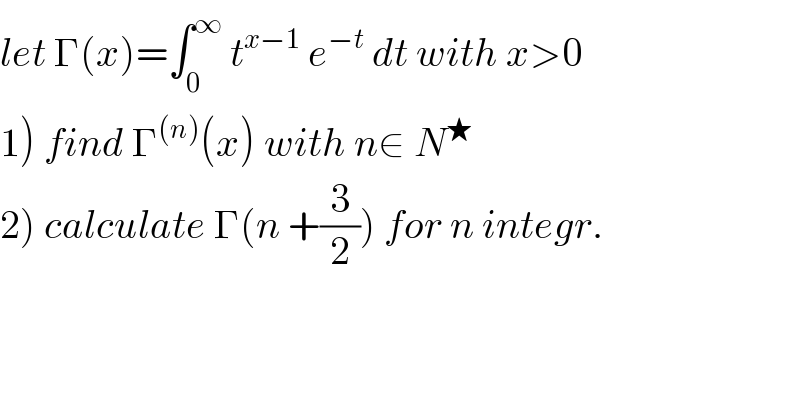
Commented by prof Abdo imad last updated on 29/Apr/18
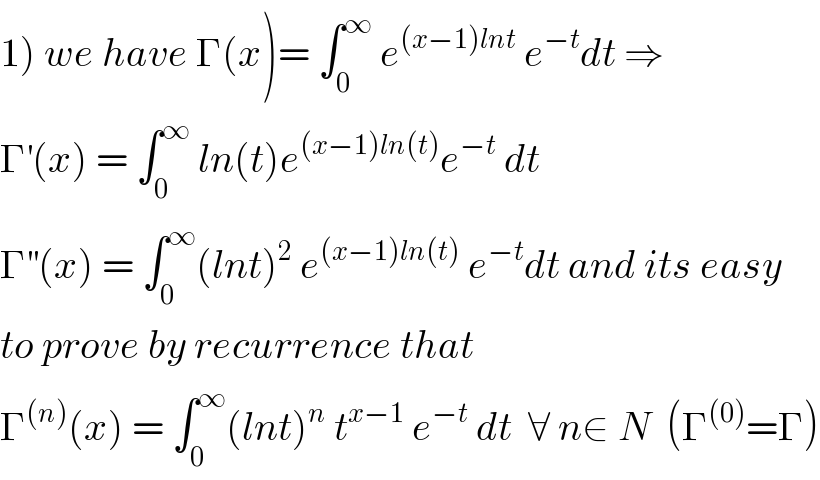
Commented by prof Abdo imad last updated on 29/Apr/18
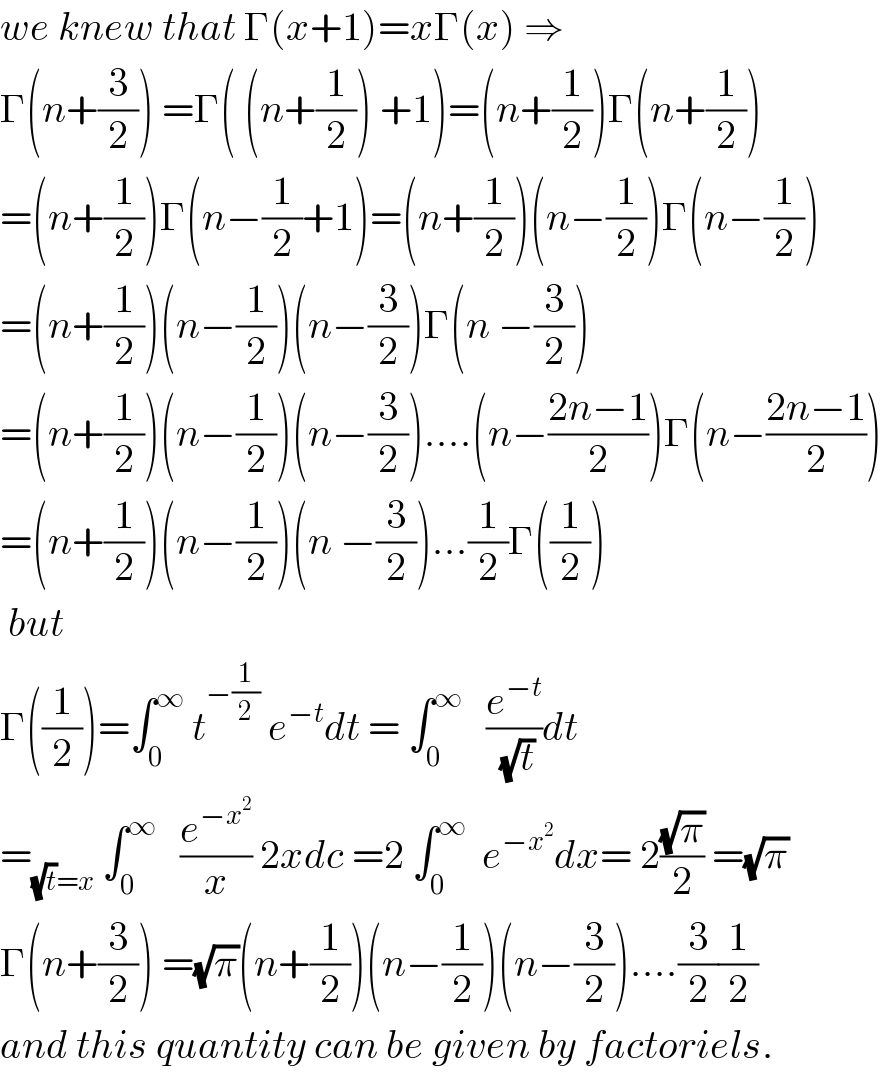
Commented by prof Abdo imad last updated on 29/Apr/18
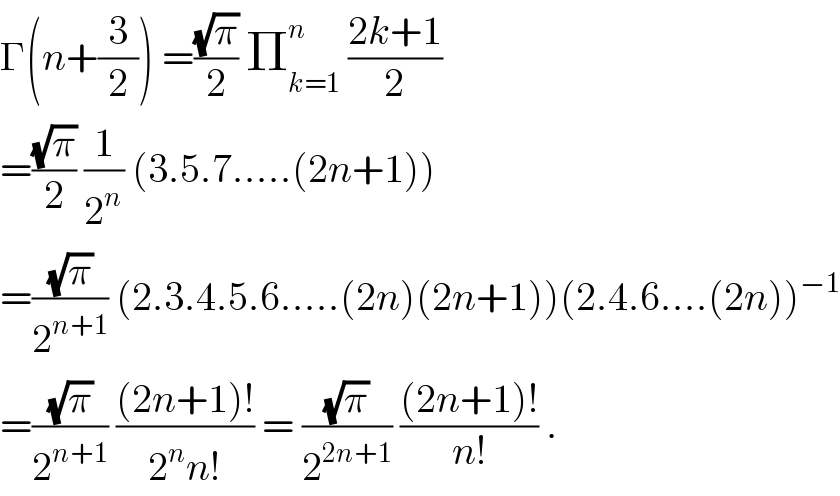
Answered by tanmay.chaudhury50@gmail.com last updated on 27/Apr/18

Answered by MJS last updated on 27/Apr/18