Question Number 34186 by Joel578 last updated on 02/May/18
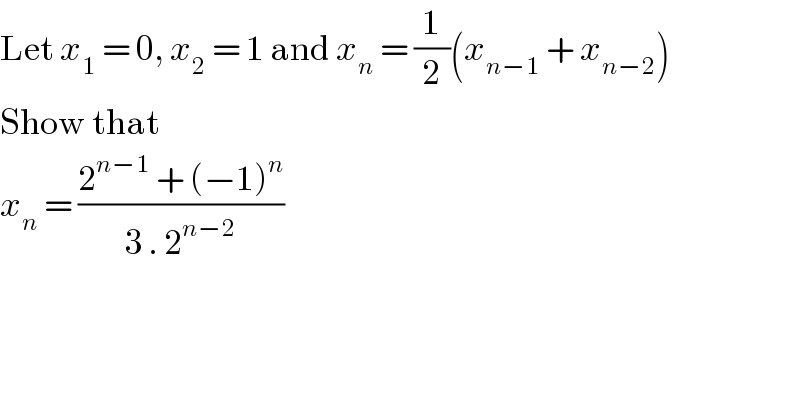
$$\mathrm{Let}\:{x}_{\mathrm{1}} \:=\:\mathrm{0},\:{x}_{\mathrm{2}} \:=\:\mathrm{1}\:\mathrm{and}\:{x}_{{n}} \:=\:\frac{\mathrm{1}}{\mathrm{2}}\left({x}_{{n}−\mathrm{1}} \:+\:{x}_{{n}−\mathrm{2}} \right) \\ $$$$\mathrm{Show}\:\mathrm{that}\: \\ $$$${x}_{{n}} \:=\:\frac{\mathrm{2}^{{n}−\mathrm{1}} \:+\:\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}\:.\:\mathrm{2}^{{n}−\mathrm{2}} } \\ $$
Commented by abdo mathsup 649 cc last updated on 02/May/18
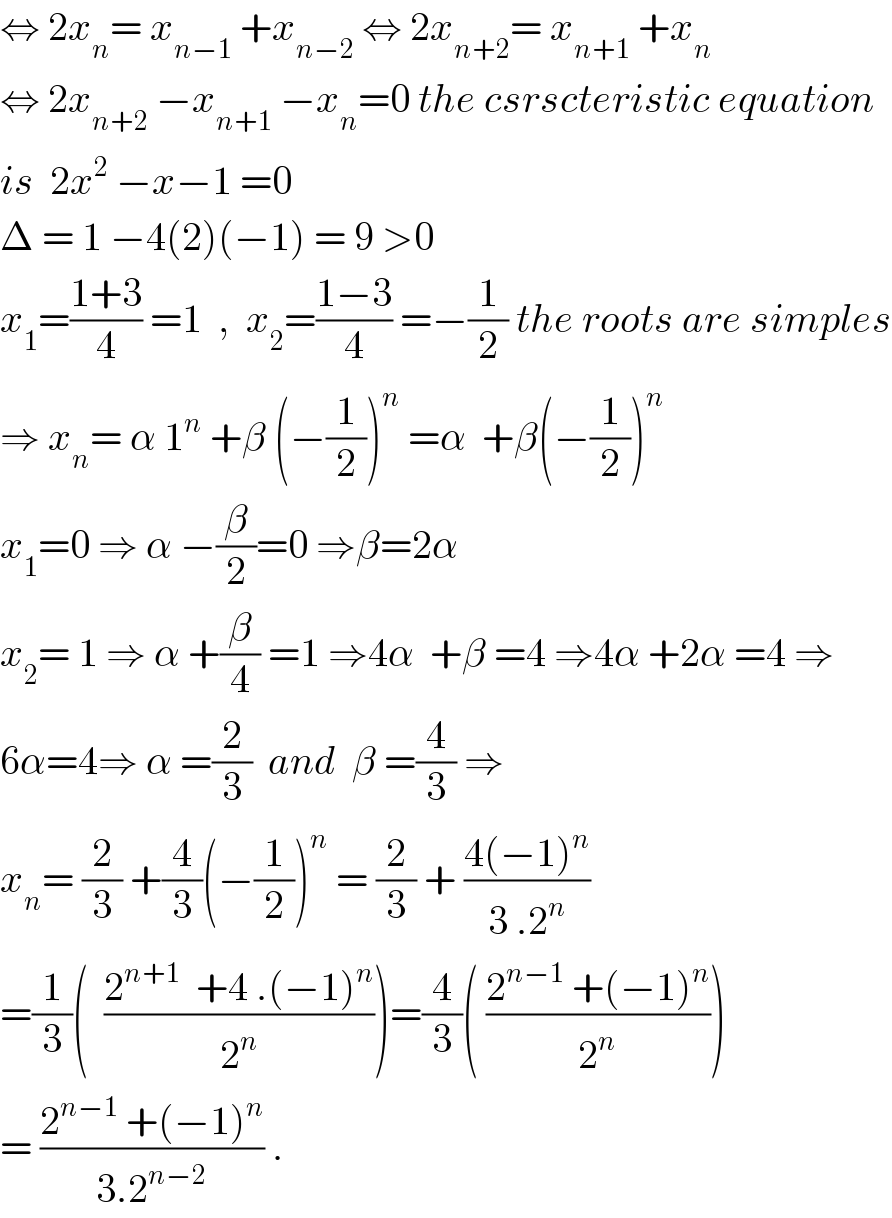
$$\Leftrightarrow\:\mathrm{2}{x}_{{n}} =\:{x}_{{n}−\mathrm{1}} \:+{x}_{{n}−\mathrm{2}} \:\Leftrightarrow\:\mathrm{2}{x}_{{n}+\mathrm{2}} =\:{x}_{{n}+\mathrm{1}} \:+{x}_{{n}} \\ $$$$\Leftrightarrow\:\mathrm{2}{x}_{{n}+\mathrm{2}} \:−{x}_{{n}+\mathrm{1}} \:−{x}_{{n}} =\mathrm{0}\:{the}\:{csrscteristic}\:{equation} \\ $$$${is}\:\:\mathrm{2}{x}^{\mathrm{2}} \:−{x}−\mathrm{1}\:=\mathrm{0} \\ $$$$\Delta\:=\:\mathrm{1}\:−\mathrm{4}\left(\mathrm{2}\right)\left(−\mathrm{1}\right)\:=\:\mathrm{9}\:>\mathrm{0} \\ $$$${x}_{\mathrm{1}} =\frac{\mathrm{1}+\mathrm{3}}{\mathrm{4}}\:=\mathrm{1}\:\:,\:\:{x}_{\mathrm{2}} =\frac{\mathrm{1}−\mathrm{3}}{\mathrm{4}}\:=−\frac{\mathrm{1}}{\mathrm{2}}\:{the}\:{roots}\:{are}\:{simples} \\ $$$$\Rightarrow\:{x}_{{n}} =\:\alpha\:\mathrm{1}^{{n}} \:+\beta\:\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \:=\alpha\:\:+\beta\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \\ $$$${x}_{\mathrm{1}} =\mathrm{0}\:\Rightarrow\:\alpha\:−\frac{\beta}{\mathrm{2}}=\mathrm{0}\:\Rightarrow\beta=\mathrm{2}\alpha \\ $$$${x}_{\mathrm{2}} =\:\mathrm{1}\:\Rightarrow\:\alpha\:+\frac{\beta}{\mathrm{4}}\:=\mathrm{1}\:\Rightarrow\mathrm{4}\alpha\:\:+\beta\:=\mathrm{4}\:\Rightarrow\mathrm{4}\alpha\:+\mathrm{2}\alpha\:=\mathrm{4}\:\Rightarrow \\ $$$$\mathrm{6}\alpha=\mathrm{4}\Rightarrow\:\alpha\:=\frac{\mathrm{2}}{\mathrm{3}}\:\:{and}\:\:\beta\:=\frac{\mathrm{4}}{\mathrm{3}}\:\Rightarrow \\ $$$${x}_{{n}} =\:\frac{\mathrm{2}}{\mathrm{3}}\:+\frac{\mathrm{4}}{\mathrm{3}}\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{{n}} \:=\:\frac{\mathrm{2}}{\mathrm{3}}\:+\:\frac{\mathrm{4}\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}\:.\mathrm{2}^{{n}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\left(\:\:\frac{\mathrm{2}^{{n}+\mathrm{1}} \:\:+\mathrm{4}\:.\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\right)=\frac{\mathrm{4}}{\mathrm{3}}\left(\:\frac{\mathrm{2}^{{n}−\mathrm{1}} \:+\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}} }\right) \\ $$$$=\:\frac{\mathrm{2}^{{n}−\mathrm{1}} \:+\left(−\mathrm{1}\right)^{{n}} }{\mathrm{3}.\mathrm{2}^{{n}−\mathrm{2}} }\:. \\ $$
Answered by candre last updated on 02/May/18
![x_1 =((2^(1−1) +(−1)^1 )/(3∙2^(1−2) ))=((1−1)/(3/2))=0 x_2 =((2^(2−1) +(−1)^2 )/(3∙2^(2−2) ))=((2+1)/3)=1 x_(n−1) =((2^(n−2) +(−1)^(n−1) )/(3∙2^(n−3) )) x_(n−2) =((2^(n−3) +(−1)^(n−2) )/(3∙2^(n−4) )) ((x_(n−1) +x_(n−2) )/2)=(1/2)(((2^(n−2) +(−1)^(n−1) )/(3∙2^(n−3) ))+((2^(n−3) +(−1)^(n−2) )/(3∙2^(n−4) ))) =(1/(2^(n+1) ∙3))(((2^(n−2) −(−1)^n )/2^(−3) )+((2^(n−3) +(−1)^n )/2^(−4) )) =(1/(2^(n+1) ∙3))[2^3 (2^(n−2) −(−1)^n )+2^4 (2^(n−3) +(−1)^n )] =((2^3 2^(n−2) −2^3 (−1)^n +2^4 2^(n−3) +2^4 (−1)^n )/(2^(n+1) ∙3)) =((2^(n+2) +(2^4 −2^3 )(−1)^n )/(2^(n+1) ∙3)) =((2^3 (2^(n−1) +(2−1)(−1)^n ))/(2^(n+1) ∙3)) =((2^(n−1) +(−1)^n )/(2^(n−2) ∙3))](https://www.tinkutara.com/question/Q34188.png)
$${x}_{\mathrm{1}} =\frac{\mathrm{2}^{\mathrm{1}−\mathrm{1}} +\left(−\mathrm{1}\right)^{\mathrm{1}} }{\mathrm{3}\centerdot\mathrm{2}^{\mathrm{1}−\mathrm{2}} }=\frac{\mathrm{1}−\mathrm{1}}{\mathrm{3}/\mathrm{2}}=\mathrm{0} \\ $$$${x}_{\mathrm{2}} =\frac{\mathrm{2}^{\mathrm{2}−\mathrm{1}} +\left(−\mathrm{1}\right)^{\mathrm{2}} }{\mathrm{3}\centerdot\mathrm{2}^{\mathrm{2}−\mathrm{2}} }=\frac{\mathrm{2}+\mathrm{1}}{\mathrm{3}}=\mathrm{1} \\ $$$${x}_{{n}−\mathrm{1}} =\frac{\mathrm{2}^{{n}−\mathrm{2}} +\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{3}\centerdot\mathrm{2}^{{n}−\mathrm{3}} } \\ $$$${x}_{{n}−\mathrm{2}} =\frac{\mathrm{2}^{{n}−\mathrm{3}} +\left(−\mathrm{1}\right)^{{n}−\mathrm{2}} }{\mathrm{3}\centerdot\mathrm{2}^{{n}−\mathrm{4}} } \\ $$$$\frac{{x}_{{n}−\mathrm{1}} +{x}_{{n}−\mathrm{2}} }{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{2}^{{n}−\mathrm{2}} +\left(−\mathrm{1}\right)^{{n}−\mathrm{1}} }{\mathrm{3}\centerdot\mathrm{2}^{{n}−\mathrm{3}} }+\frac{\mathrm{2}^{{n}−\mathrm{3}} +\left(−\mathrm{1}\right)^{{n}−\mathrm{2}} }{\mathrm{3}\centerdot\mathrm{2}^{{n}−\mathrm{4}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} \centerdot\mathrm{3}}\left(\frac{\mathrm{2}^{{n}−\mathrm{2}} −\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{−\mathrm{3}} }+\frac{\mathrm{2}^{{n}−\mathrm{3}} +\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{−\mathrm{4}} }\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}^{{n}+\mathrm{1}} \centerdot\mathrm{3}}\left[\mathrm{2}^{\mathrm{3}} \left(\mathrm{2}^{{n}−\mathrm{2}} −\left(−\mathrm{1}\right)^{{n}} \right)+\mathrm{2}^{\mathrm{4}} \left(\mathrm{2}^{{n}−\mathrm{3}} +\left(−\mathrm{1}\right)^{{n}} \right)\right] \\ $$$$=\frac{\mathrm{2}^{\mathrm{3}} \mathrm{2}^{{n}−\mathrm{2}} −\mathrm{2}^{\mathrm{3}} \left(−\mathrm{1}\right)^{{n}} +\mathrm{2}^{\mathrm{4}} \mathrm{2}^{{n}−\mathrm{3}} +\mathrm{2}^{\mathrm{4}} \left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}+\mathrm{1}} \centerdot\mathrm{3}} \\ $$$$=\frac{\mathrm{2}^{{n}+\mathrm{2}} +\left(\mathrm{2}^{\mathrm{4}} −\mathrm{2}^{\mathrm{3}} \right)\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}+\mathrm{1}} \centerdot\mathrm{3}} \\ $$$$=\frac{\mathrm{2}^{\mathrm{3}} \left(\mathrm{2}^{{n}−\mathrm{1}} +\left(\mathrm{2}−\mathrm{1}\right)\left(−\mathrm{1}\right)^{{n}} \right)}{\mathrm{2}^{{n}+\mathrm{1}} \centerdot\mathrm{3}} \\ $$$$=\frac{\mathrm{2}^{{n}−\mathrm{1}} +\left(−\mathrm{1}\right)^{{n}} }{\mathrm{2}^{{n}−\mathrm{2}} \centerdot\mathrm{3}} \\ $$
