Question Number 33353 by caravan msup abdo. last updated on 15/Apr/18
![let x∈]1,+∞[ andλ ∈[−1,1] give the integral ∫_0 ^∞ ((t^(x−1) e^(−t) )/(1−λe^(−t) )) dt at form of serie.](https://www.tinkutara.com/question/Q33353.png)
$$\left.{let}\:{x}\in\right]\mathrm{1},+\infty\left[\:{and}\lambda\:\in\left[−\mathrm{1},\mathrm{1}\right]\right. \\ $$$${give}\:{the}\:{integral}\:\int_{\mathrm{0}} ^{\infty} \:\frac{{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} }{\mathrm{1}−\lambda{e}^{−{t}} }\:{dt} \\ $$$${at}\:{form}\:{of}\:{serie}. \\ $$
Commented by math khazana by abdo last updated on 18/Apr/18
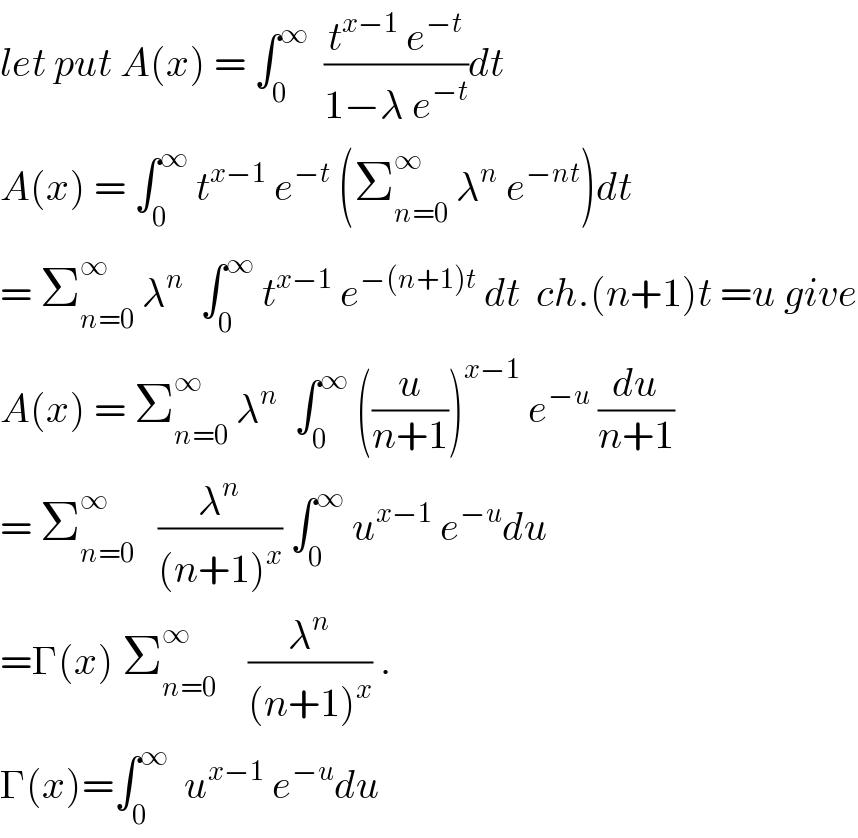
$${let}\:{put}\:{A}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} }{\mathrm{1}−\lambda\:{e}^{−{t}} }{dt} \\ $$$${A}\left({x}\right)\:=\:\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} \:{e}^{−{t}} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\lambda^{{n}} \:{e}^{−{nt}} \right){dt} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\lambda^{{n}} \:\:\int_{\mathrm{0}} ^{\infty} \:{t}^{{x}−\mathrm{1}} \:{e}^{−\left({n}+\mathrm{1}\right){t}} \:{dt}\:\:{ch}.\left({n}+\mathrm{1}\right){t}\:={u}\:{give} \\ $$$${A}\left({x}\right)\:=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\lambda^{{n}} \:\:\int_{\mathrm{0}} ^{\infty} \:\left(\frac{{u}}{{n}+\mathrm{1}}\right)^{{x}−\mathrm{1}} \:{e}^{−{u}} \:\frac{{du}}{{n}+\mathrm{1}} \\ $$$$=\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\lambda^{{n}} }{\left({n}+\mathrm{1}\right)^{{x}} }\:\int_{\mathrm{0}} ^{\infty} \:{u}^{{x}−\mathrm{1}} \:{e}^{−{u}} {du} \\ $$$$=\Gamma\left({x}\right)\:\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\:\frac{\lambda^{{n}} }{\left({n}+\mathrm{1}\right)^{{x}} }\:. \\ $$$$\Gamma\left({x}\right)=\int_{\mathrm{0}} ^{\infty} \:\:{u}^{{x}−\mathrm{1}} \:{e}^{−{u}} {du} \\ $$
